题目内容
14．由一排编号为1至7的七个座位连成一排，现有2名语文老师和2名数学老师共4人就坐，要求同一学科的老师不能相邻，有多少种不同的坐法（ ）| A． | 400 | B． | 330 | C． | 440 | D． | 324 |
分析 记X为语文老师，Y为数学老师，O为空位，主要是XXYY的顺序分类：求出（1）第一类属于XYXY，或YXYX型的数量，求出（2）第二类XYYX类的数量，求出（3）第三类：XXYY的数量，再把这三个数量相加，即得所求．
解答 解：记X为语文老师，Y为数学老师，O为空位，主要是XXYY的顺序分类：
（1）第一类属于XYXY，或YXYX型的有：${C}_{7}^{4}$×4+${C}_{7}^{4}$×4=280种．
（2）第二类属于 XYYX 型，再分三种类型：①属于XYOYXOO型的有${C}_{5}^{2}$×8=80种；②属于XYOOYXO型的有4×8=32种；③属于XYOOOYX型的有8种．
（3）第三类属于XXYY型，再有两类：①属于XOXYOYO型的有3×8=24，②属于XOXYOOY型的有2×8=16种，
因此共有：280+80+32+8+24+16=440种，
故选：C．
点评 本题主要考查排列与组合及两个基本原理，体现了分类讨论的数学思想，注意分类的层次，属于中档题．
练习册系列答案
相关题目
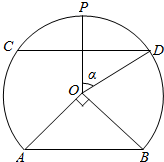如图是一个弓形APB湖面景点的平面示意图．其所在圆O的半径为$\sqrt{2}$（圆心O在弓形APB内），P点是AB弧的中点，C为圆周上靠近A的一点，D为圆周上靠近B的一点，且CD∥AB．现在准备从A经过C到D建造一条观光路线，其中A到C是圆弧AC，C到D是线段CD．设∠AOB=$\frac{π}{2}$，∠POD=α rad，观光路线总长为y km．
19．设[x]表示不超过实数x的最大整数，如[2.6]=2，[-2.6]=-3，设g（x）=$\frac{{a}^{x}}{{a}^{x}+1}$（a＞0且a≠1），那么函数f（x）=[g（x）-$\frac{1}{2}$]+[g（-x）-$\frac{1}{2}$]的值域为（ ）
| A． | {-1，0，1} | B． | {0，1} | C． | {1，-1} | D． | {-1，0} |
3．已知ξ的分别列如下：
并且η=2ξ+3，则方差Dη=$\frac{139}{36}$．
| ξ | 1 | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ |