题目内容
16.函数f(x)=$\sqrt{cosx}$+$\frac{1}{\sqrt{sinx}}$的定义域是(2kπ,2kπ+$\frac{π}{2}$],k∈Z.分析 根据函数成立的条件即可求函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{cosx≥0}\\{sinx>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{2kπ-\frac{π}{2}≤x≤2kπ+\frac{π}{2},k∈Z}\\{2kπ<x<2kπ+π,k∈Z}\end{array}\right.$,
解得2kπ<x≤2kπ+$\frac{π}{2}$,k∈Z,
即函数的定义域为(2kπ,2kπ+$\frac{π}{2}$],k∈Z,
故答案为:(2kπ,2kπ+$\frac{π}{2}$],k∈Z
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
11.设集合M={2,1-3a,a2+1},N={a2+a-4,2a+1,-1},且M∩N={2},则a的取值范围是( )
| A. | {$\frac{1}{2}$} | B. | {2,-3} | C. | {-3,$\frac{1}{2}$} | D. | {-3,2,$\frac{1}{2}$} |
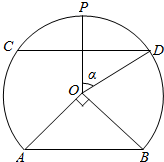 如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.
如图是一个弓形APB湖面景点的平面示意图.其所在圆O的半径为$\sqrt{2}$(圆心O在弓形APB内),P点是AB弧的中点,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB.现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧AC,C到D是线段CD.设∠AOB=$\frac{π}{2}$,∠POD=α rad,观光路线总长为y km.