题目内容
14.已知直线y=2x+1与圆x2+y2+mx=0没有公共点,则m的取值范围是( )| A. | (4-2$\sqrt{5}$,4+2$\sqrt{5}$) | B. | (4-2$\sqrt{5}$,0)∪(0,4+2$\sqrt{5}$) | C. | (-4-2$\sqrt{5}$,-4+2$\sqrt{5}$) | D. | (-4-2$\sqrt{5}$,0)∪(0,-4+2$\sqrt{5}$) |
分析 根据直线与圆没有公共点得到直线与圆的位置关系是相离,则根据圆心到直线的距离大于半径列出关于m的不等式,解不等式即可得到m的范围.
解答 解:把圆x2+y2+mx=0化为标准方程为(x+$\frac{m}{2}$)2+y2=$\frac{{m}^{2}}{4}$,所以圆心(-$\frac{m}{2}$,0),半径r=|$\frac{m}{2}$|,
由直线与圆没有公共点得到:圆心到直线y=2x+1的距离d=$\frac{|m+1|}{\sqrt{5}}$>r=|$\frac{m}{2}$|,
∴m的范围是(-4-2$\sqrt{5}$,0)∪(0,-4+2$\sqrt{5}$).
故选:D.
点评 此题考查学生掌握直线与圆相离时所满足的条件,灵活运用点到直线的距离公式化简求值,会把绝对值不等式转化为一般的二次不等式进行求解

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,若f(a)=$\frac{1}{4}$,则a的值为( )
| A. | -2或$\frac{1}{4}$ | B. | $\root{4}{2}或-2$ | C. | -2 | D. | $\root{4}{2}$ |
9.同时抛掷8枚质地均匀的相同硬币,则出现正面向上的硬币数X的方差为( )
| A. | 4 | B. | $\frac{1}{2}$ | C. | 2 | D. | 1 |
6.已知cosα=$\frac{3}{5}$,则sin2α+cos2α的值为( )
| A. | $\frac{9}{25}$ | B. | $\frac{18}{25}$ | C. | $\frac{23}{25}$ | D. | $\frac{34}{25}$ |
3.执行如图所示的程序框图,若输出的结果是27,则输入的数是( )
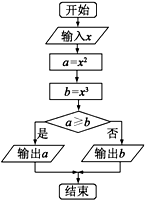

| A. | -3或-3$\sqrt{3}$ | B. | 3或-3$\sqrt{3}$ | C. | -3或3$\sqrt{3}$ | D. | 3或3$\sqrt{3}$ |