题目内容
9．同时抛掷8枚质地均匀的相同硬币，则出现正面向上的硬币数X的方差为（ ）| A． | 4 | B． | $\frac{1}{2}$ | C． | 2 | D． | 1 |
分析 利用题意判断得出服从B～（8，$\frac{1}{2}$），利用独立重复试验的方差求解即可．
解答 解：根据题意得出：B～（8，$\frac{1}{2}$），
P（X=k）=${C}_{8}^{k}$（$\frac{1}{2}$）k•（1-$\frac{1}{2}$）8-k，
出现正面向上的硬币数X的方差：8×$\frac{1}{2}$×（1-$\frac{1}{2}$）=2，
故选；C
点评 本题考查概率的求法，n次独立重复实验中恰好发生k次的概率，是基础题，解题时要认真审题，注意相互独立事件同时发生的概率计算公式的灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．直线ax+by+c=0与圆x2+y2=9相交于两点M、N，若c2=a2+b2，则|MN|=（ ）
| A． | 4$\sqrt{2}$ | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{10}$ | D． | $\sqrt{10}$ |
20．已知角α的终边经过点$P（{-1，-\sqrt{3}}）$，则tanα等于（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | -$\sqrt{3}$ | C． | $\sqrt{3}$ | D． | -$\frac{1}{2}$ |
14．已知直线y=2x+1与圆x2+y2+mx=0没有公共点，则m的取值范围是（ ）
| A． | （4-2$\sqrt{5}$，4+2$\sqrt{5}$） | B． | （4-2$\sqrt{5}$，0）∪（0，4+2$\sqrt{5}$） | C． | （-4-2$\sqrt{5}$，-4+2$\sqrt{5}$） | D． | （-4-2$\sqrt{5}$，0）∪（0，-4+2$\sqrt{5}$） |
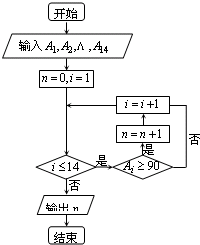某高三学生进入高中三年来的第1次至14次数学考试成绩分别为：79，83，93，86，99，98，94，88，98，91，95，103，101，114，依次记为A1，A2…，A14．如图是成绩在一定范围内考试次数的一个算法流程图．那么输出的结果是（ ）