题目内容
6.已知cosα=$\frac{3}{5}$,则sin2α+cos2α的值为( )| A. | $\frac{9}{25}$ | B. | $\frac{18}{25}$ | C. | $\frac{23}{25}$ | D. | $\frac{34}{25}$ |
分析 由cosα的值,利用同角三角函数间的基本关系求出sin2α的值,原式变形后代入计算即可求出值.
解答 解:∵cosα=$\frac{3}{5}$,
∴sin2α=1-cos2α=$\frac{16}{25}$,
则原式=sin2α+1-2sin2α=1-sin2α=$\frac{9}{25}$,
故选:A.
点评 此题考查了二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
14.已知直线y=2x+1与圆x2+y2+mx=0没有公共点,则m的取值范围是( )
| A. | (4-2$\sqrt{5}$,4+2$\sqrt{5}$) | B. | (4-2$\sqrt{5}$,0)∪(0,4+2$\sqrt{5}$) | C. | (-4-2$\sqrt{5}$,-4+2$\sqrt{5}$) | D. | (-4-2$\sqrt{5}$,0)∪(0,-4+2$\sqrt{5}$) |
11.某赛季,甲、乙两名篮球运动员都参加了10场比赛,比赛得分情况记录如下:
(Ⅰ)求甲10场比赛得分的中位数;
(Ⅱ)求乙10场比赛得分的方差.
| 甲 | 10 | 30 | 47 | 28 | 46 | 14 | 26 | 11 | 43 | 46 |
| 乙 | 37 | 21 | 31 | 29 | 19 | 32 | 23 | 25 | 20 | 33 |
(Ⅱ)求乙10场比赛得分的方差.
15.某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-$\sqrt{3}$cos$\frac{π}{12}$t-sin$\frac{π}{12}$t,t∈[0,24).若要求实验室温度不高于11℃,则实验室需要降温的时间为( )
| A. | (9,17) | B. | (10,18) | C. | (11,19) | D. | (12,20) |
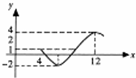 +c(A>0,ω>0,φ>0)图象的一部分.
+c(A>0,ω>0,φ>0)图象的一部分. 某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )
某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )