题目内容
若函数y=f(x)在R上可导,且满足不等式xf′(x)>-f(x)恒成立,且常数a,b满足a>b,则下列不等式一定成立的是 ( )
| A.af(b)>bf(a) | B.af(a)>bf(b) |
| C.af(a)<bf(b) | D.af(b)<bf(a) |
B
令F(x)=xf(x),
则F′(x)=xf′(x)+f(x),由xf′(x)>-f(x),
得xf′(x)+f(x)>0,
即F′(x)>0,
所以F(x)在R上为递增函数.
因为a>b,所以af(a)>bf(b).
则F′(x)=xf′(x)+f(x),由xf′(x)>-f(x),
得xf′(x)+f(x)>0,
即F′(x)>0,
所以F(x)在R上为递增函数.
因为a>b,所以af(a)>bf(b).

练习册系列答案
相关题目
 .
.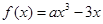 .
.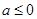 时,求函数
时,求函数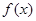 单调区间;
单调区间;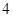 ,求
,求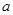 的值.
的值.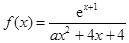 ,其中
,其中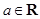 .
.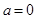 ,求函数
,求函数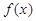 的极值;
的极值;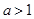 时,试确定函数
时,试确定函数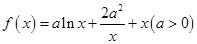 .若曲线
.若曲线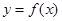 在点
在点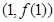 处的切线与直线
处的切线与直线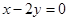 垂直,
垂直,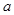 的值;
的值;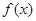 的单调区间;
的单调区间;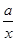 .
.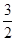 ,求实数a的值;
,求实数a的值;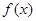 满足
满足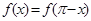 且当
且当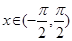 时,
时,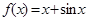 ,则( )
,则( )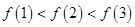
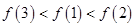
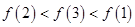
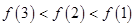
 .
. 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数 x2
x2 ㏑x的单调递减区间为( )
㏑x的单调递减区间为( ) 1,1]
1,1]