题目内容
已知函数f(x)=x3-ax2-3x.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)的单调区间.
(1)a≤0
(2)f(x)的单调递增区间为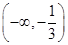 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为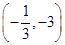 .
.
(2)f(x)的单调递增区间为
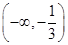 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为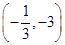 .
.解:(1)对f(x)求导,
得f′(x)=3x2-2ax-3.
由f′(x)≥0,得a≤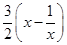 .
.
记t(x)=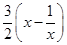 ,当x≥1时,t(x)是增函数,
,当x≥1时,t(x)是增函数,
∴t(x)min=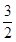 (1-1)=0.∴a≤0.
(1-1)=0.∴a≤0.
(2)由题意,得f′(3)=0,
即27-6a-3=0,
∴a=4.∴f(x)=x3-4x2-3x,
f′(x)=3x2-8x-3.
令f′(x)=0,得x1=-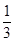 ,x2=3.
,x2=3.
当x变化时,f′(x)、f(x)的变化情况如下表:
∴f(x)的单调递增区间为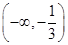 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为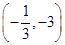 .
.
得f′(x)=3x2-2ax-3.
由f′(x)≥0,得a≤
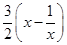 .
.记t(x)=
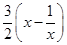 ,当x≥1时,t(x)是增函数,
,当x≥1时,t(x)是增函数,∴t(x)min=
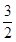 (1-1)=0.∴a≤0.
(1-1)=0.∴a≤0.(2)由题意,得f′(3)=0,
即27-6a-3=0,
∴a=4.∴f(x)=x3-4x2-3x,
f′(x)=3x2-8x-3.
令f′(x)=0,得x1=-
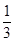 ,x2=3.
,x2=3.当x变化时,f′(x)、f(x)的变化情况如下表:
| x | 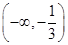 | -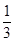 | 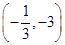 | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ? | 极大值 | ? | 极小值 | ? |
∴f(x)的单调递增区间为
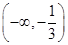 ,[3,+∞),f(x)的单调递减区间为
,[3,+∞),f(x)的单调递减区间为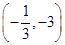 .
.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
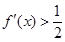 ,则满足
,则满足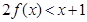 的x的集合为( )
的x的集合为( )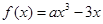 .
.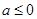 时,求函数
时,求函数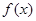 单调区间;
单调区间;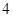 ,求
,求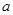 的值.
的值.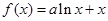 ,对任意的
,对任意的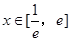 时,
时,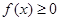 恒成立,则a的范围为 .
恒成立,则a的范围为 .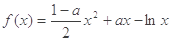 (
( )
) 时,求函数
时,求函数 的极值;(2)当
的极值;(2)当 时,讨论
时,讨论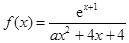 ,其中
,其中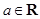 .
.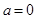 ,求函数
,求函数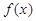 的极值;
的极值;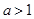 时,试确定函数
时,试确定函数 .
. 在
在 上为减函数,求实数
上为减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数