题目内容
【题目】函数 ![]() .
.
(1)求函数 ![]() 的最大值;
的最大值;
(2)对于任意 ![]() ,且
,且 ![]() ,是否存在实数
,是否存在实数 ![]() ,使
,使 ![]() 恒成立,若存在求出
恒成立,若存在求出 ![]() 的范围,若不存在,说明理由;
的范围,若不存在,说明理由;
(3)若正项数列 ![]() 满足
满足 ![]() ,且数列
,且数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,试判断
,试判断 ![]() 与
与 ![]() 的大小,并加以证明.
的大小,并加以证明.
【答案】
(1)解: ![]() ,
,
则 ![]() ,
,
所以 ![]() 函数单调递减,
函数单调递减, ![]() 函数单调递增.
函数单调递增.
从而 ![]()
(2)解:若 ![]() 恒成立,
恒成立,
则 ![]() ,
,
设函数 ![]() ,又
,又 ![]() ,
,
则只需函数 ![]() 在
在 ![]() 上为单调递减函数,
上为单调递减函数,
即 ![]() 在
在 ![]() 上恒成立,
上恒成立,
则 ![]() ,
,
记 ![]() ,则
,则 ![]() ,从而
,从而 ![]() 在
在 ![]() 上单调递减,在
上单调递减,在 ![]() 单调递增,
单调递增,
故 ![]() ,
,
则存在 ![]() ,使得不等式恒成立
,使得不等式恒成立
(3)解:由 ![]() .
.
即 ![]() ,由
,由 ![]() ,得
,得 ![]() ,
,
因为 ![]() ,由(1)知
,由(1)知 ![]() 时,
时, ![]() ,
,
故 ![]() ,
,![]() 即
即 ![]()
【解析】(1)首先求出函数的定义域以及导函数,根据导数符号即可求出原函数的单调性即可求出最大值。(2)根据题意结合函数的单调性和其导函数的关系,即可得到 φ ′ ( x ) ≤ 0 恒成立,分离出参数m后化为求函数最值即可并利用导数求得函数的最值。(3)整理数列的代数式求出数列 { an}的通项公式根据题意代入即可得到 a n> ln ( an + 1 ),进而得到Sn的表达式结合对数的性质由裂项相消法即可得出结果。
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和数列的前n项和的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;数列{an}的前n项和sn与通项an的关系
在这个区间单调递减;数列{an}的前n项和sn与通项an的关系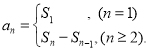 .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目