题目内容
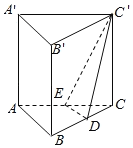
【题目】如图,在正三棱柱![]() 中,底面
中,底面![]() 边长为2,
边长为2,![]() 为
为![]() 的中点,三棱柱
的中点,三棱柱![]() 的体积.
的体积.

(1)求三棱柱的表面积;
(2)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)由三棱柱体积![]() ,求出高AA′=3,由此能求出三棱柱的表面积;(2)取AC中点E,连结DE、C′E,由D为BC中点,得DE∥AB,从而∠C′DE是异面直线AB与C′D所成角(或所成角的补角),由此能求出异面直线AB与C′D所成角的余弦值.
,求出高AA′=3,由此能求出三棱柱的表面积;(2)取AC中点E,连结DE、C′E,由D为BC中点,得DE∥AB,从而∠C′DE是异面直线AB与C′D所成角(或所成角的补角),由此能求出异面直线AB与C′D所成角的余弦值.
详解:(1)∵在正三棱柱ABC﹣A′B′C′中,底面△ABC边长为2,D为BC的中点,三棱柱体积![]() ,
,
![]()
解得高AA′=3,
∴三棱柱的表面积:![]() =
= ![]() ;
;
(2)取AC中点E,连结DE、C′E,
∵D为BC中点,∴DE∥AB,
∴∠C′DE是异面直线AB与C′D所成角(或所成角的补角),
∵DE=![]() AB=1,C′D=C′E=
AB=1,C′D=C′E=![]() =
=![]() =
=![]() ,
,
∴cos∠C′DE=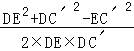 =
=![]() =
=![]() .
.

练习册系列答案
相关题目