题目内容
【题目】已知椭圆![]() ,离心率
,离心率![]() ,点
,点![]() 在椭圆上.
在椭圆上.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上一点,左顶点为
上一点,左顶点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() 为定值.
为定值.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)根据椭圆离心率![]() ,点
,点![]() 在椭圆上,结合性质
在椭圆上,结合性质![]() , ,列出关于
, ,列出关于![]() 、
、![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的标准方程;(2)设
的标准方程;(2)设![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,由
,由![]() 三点共线,可得
三点共线,可得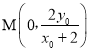 ,
, 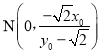 ,则
,则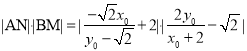 ,结合
,结合![]() ,消去
,消去![]() 可得
可得![]() 为定值
为定值![]() .
.
试题解析:(1)依题意得![]() ,设
,设![]() ,则
,则![]() ,
,
由点![]() 在椭圆上,有
在椭圆上,有![]() ,解得
,解得![]() ,则
,则![]() ,
,
椭圆C的方程为: ![]() .
.
(2)设![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,由APM三点共线,则有
,由APM三点共线,则有![]() ,即
,即![]() ,解得
,解得![]() ,则
,则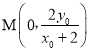 ,
,
由BPN三点共线,有![]() ,即
,即![]() ,解得
,解得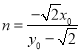 ,
,
则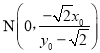
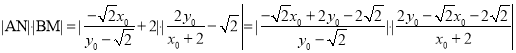
=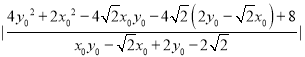
又点P在椭圆上,满足![]() ,有
,有![]() ,
,
代入上式得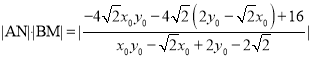
=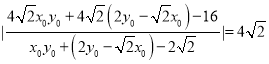 ,
,
可知![]() 为定值
为定值![]() .
.

练习册系列答案
相关题目
【题目】某同学参加社会实践活动,随机调查了某小区5个家庭的年可支配收入x(单位:万元)与年家庭消费y(单位:万元)的数据,制作了对照表:
x/万元 | 2.7 | 2.8 | 3.1 | 3.5 | 3.9 |
y/万元 | 1.4 | 1.5 | 1.6 | 1.8 | 2.2 |
由表中数据得回归直线方程为![]() ,得到下列结论,其中正确的是( )
,得到下列结论,其中正确的是( )
A.若某户年可支配收入为4万元时,则年家庭消费约为2.3万元
B.若某户年可支配收入为4万元时,则年家庭消费约为2.1万元
C.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.5万元
D.若年可支配收入每增加1万元,则年家庭消费相应平均增加0.1万元






