题目内容
已知抛物线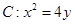 的焦点为
的焦点为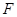 ,过点
,过点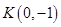 的直线
的直线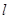 与
与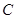 相交于
相交于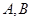 两点,点
两点,点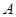 关于
关于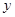 轴的对称点为
轴的对称点为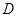 .
.
(Ⅰ)证明:点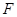 在直线
在直线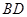 上;
上;
(Ⅱ)设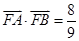 ,求
,求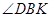 的平分线与
的平分线与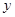 轴的交点坐标.
轴的交点坐标.
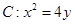 的焦点为
的焦点为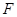 ,过点
,过点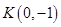 的直线
的直线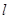 与
与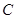 相交于
相交于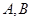 两点,点
两点,点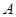 关于
关于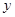 轴的对称点为
轴的对称点为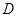 .
.(Ⅰ)证明:点
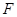 在直线
在直线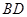 上;
上;(Ⅱ)设
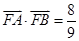 ,求
,求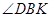 的平分线与
的平分线与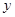 轴的交点坐标.
轴的交点坐标.(Ⅰ)解:设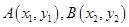 ,
,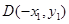 ,
,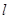 的方程为
的方程为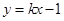 ,
,
由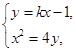 得
得 ,
,
从而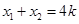 ,
,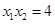 . ………2分
. ………2分
直线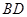 的方程为
的方程为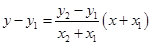 ,即
,即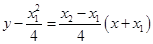 ,
,
令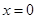 ,得
,得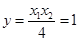 ,所以点
,所以点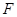 在直线
在直线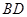 上. …………6分
上. …………6分
(Ⅱ)解:因为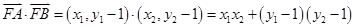
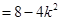 ,
,
故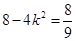 ,解得
,解得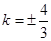 , …………9分
, …………9分
所以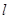 的方程为
的方程为 .
.
又由(Ⅰ)得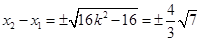 ,故直线
,故直线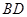 的
的 斜率为
斜率为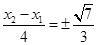 ,
,
因而直线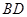 的方程为
的方程为
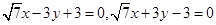 . ……12分
. ……12分
设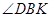 的平分线与
的平分线与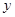 轴的交点为
轴的交点为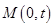 ,
,
则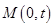 到
到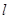 及
及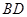 的距离分别为
的距离分别为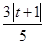 ,
, ,
,
由 ,得
,得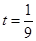 ,或
,或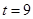 (舍去),
(舍去),
所以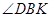 的平分线与
的平分线与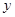 轴的交点为
轴的交点为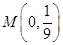 .
.
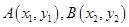 ,
,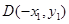 ,
,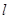 的方程为
的方程为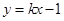 ,
,由
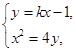 得
得 ,
,从而
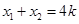 ,
,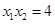 . ………2分
. ………2分直线
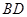 的方程为
的方程为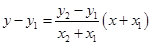 ,即
,即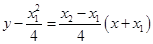 ,
,令
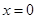 ,得
,得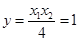 ,所以点
,所以点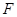 在直线
在直线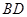 上. …………6分
上. …………6分(Ⅱ)解:因为
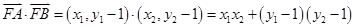
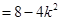 ,
,故
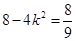 ,解得
,解得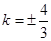 , …………9分
, …………9分所以
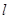 的方程为
的方程为 .
.又由(Ⅰ)得
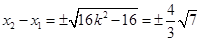 ,故直线
,故直线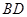 的
的 斜率为
斜率为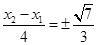 ,
,因而直线
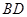 的方程为
的方程为
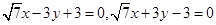 . ……12分
. ……12分设
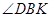 的平分线与
的平分线与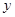 轴的交点为
轴的交点为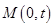 ,
,则
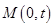 到
到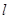 及
及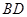 的距离分别为
的距离分别为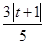 ,
, ,
,由
 ,得
,得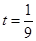 ,或
,或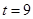 (舍去),
(舍去),所以
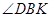 的平分线与
的平分线与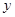 轴的交点为
轴的交点为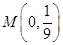 .
.略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的焦点坐标是 ( )
的焦点坐标是 ( )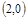

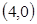

 的焦点坐标为: .
的焦点坐标为: .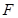 是抛物线
是抛物线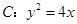 的焦点,过
的焦点,过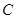 于
于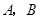 两点.则
两点.则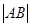 的值等于 .
的值等于 .  若x≥0,则动点
若x≥0,则动点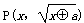 的轨迹是
的轨迹是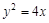 的焦点的直线
的焦点的直线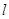 交抛物线于
交抛物线于 两点,如果
两点,如果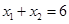 ,则
,则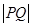 ( )
( )  与抛物线
与抛物线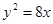 交于不同两点
交于不同两点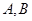 ,若线段
,若线段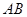 中点的纵坐标为
中点的纵坐标为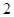 ,则
,则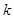 等于( )
等于( )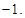
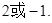
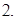
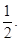
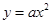 的焦点坐标为
的焦点坐标为 ,则
,则 的值为
的值为 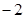
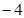
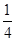
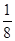
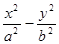 =1的一个焦点,并且这条准线与双曲线的两焦点的连线垂直,拋物线与双曲线交于点P
=1的一个焦点,并且这条准线与双曲线的两焦点的连线垂直,拋物线与双曲线交于点P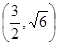 ,求拋物线方程和双曲线方程.
,求拋物线方程和双曲线方程.