题目内容
求和Sn=12+22x+32x2+…+n2xn-1,(x≠0,n∈N*).
Sn=

(1)当x=1时,Sn=12+22+32+…+n2=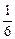 n(n+1)(2n+1),
n(n+1)(2n+1),
当x≠1时,1+2x+3x2+…+nxn-1=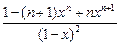 ,
,
两边同乘以x,得
x+2x2+3x2+…+nxn=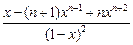
两边对x求导,得
Sn=12+22x2+32x2+…+n2xn-1
=
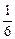 n(n+1)(2n+1),
n(n+1)(2n+1),当x≠1时,1+2x+3x2+…+nxn-1=
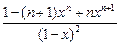 ,
,两边同乘以x,得
x+2x2+3x2+…+nxn=
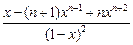
两边对x求导,得
Sn=12+22x2+32x2+…+n2xn-1
=


练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
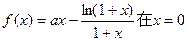 处取得极值.
处取得极值.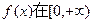 上的单调性;
上的单调性;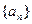 满足
满足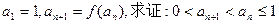 ;
;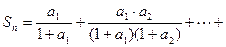
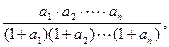
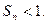
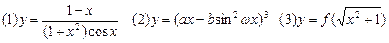
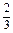 .
.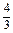 .
.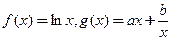 ,它们的图象在
,它们的图象在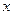 轴上的公共点处有公切线,则当
轴上的公共点处有公切线,则当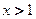 时,
时,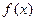 与
与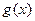 的大小关系是 ( )
的大小关系是 ( )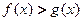
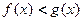

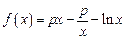 ,
,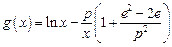 ,其中
,其中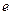 为无理数
为无理数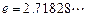 .(1)若
.(1)若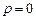 ,求证:
,求证: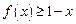 ;(2)若
;(2)若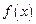 在其定义域内是单调函数,求
在其定义域内是单调函数,求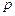 的取值范围;(3)对于区间(1,2)中的任意常数
的取值范围;(3)对于区间(1,2)中的任意常数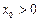 使
使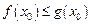 成立?
成立?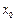 ;否则,说明理由.
;否则,说明理由.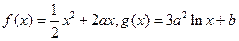 ,其中
,其中 。设两曲线
。设两曲线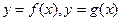 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。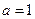 ,求
,求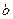 的值;
的值;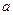 表示
表示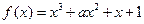 ,
,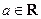 .
.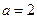 时,求函数
时,求函数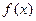 的单调区间;(Ⅱ)设函数
的单调区间;(Ⅱ)设函数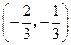 内是减函数,求
内是减函数,求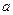 的取值范围.
的取值范围.
 ,求
,求 .
.