Question

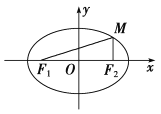
【题目】已知椭圆的离心率为，过点的椭圆的两条切线相互垂直.

（Ⅰ）求椭圆的方程；

（Ⅱ）在椭圆上是否存在这样的点，过点引抛物线的两条切线，切点分别为，且直线过点？若存在，指出这样的点有几个（不必求出点的坐标）；若不存在，请说明理由.

Answer 1

【答案】(Ⅰ)；(Ⅱ)满足条件的点有两个.

【解析】

试题

(1) 结合椭圆的离心率可求得，则椭圆方程为.

(2)由题意首先求得切线方程的参数形式，据此可得直线的方程为，则点的轨迹方程为，原问题转化为直线与椭圆的交点个数，即满足条件的点有两个.

试题解析：

（Ⅰ）由椭圆的对称性，不妨设在轴上方的切点为，轴下方的切点为，

则，的直线方程为，

因为椭圆 的离心率为，

所以椭圆，

所以 ，则，

所以椭圆方程为.

（Ⅱ）设点，，，

由，即，得，

∴抛物线在点处的切线的方程为，

即，

∵，∴.

∵点在切线上，∴.①

同理，.②

综合①、②得，点，的坐标都满足方程.

∵经过，两点的直线是唯一的，

∴直线的方程为，

∵点在直线上，∴，

∴点的轨迹方程为.

又∵点在椭圆上，又在直线上，

∴直线经过椭圆内一点，

∴直线与椭圆交于两点.

∴满足条件的点有两个.