题目内容
【题目】已知函数![]() ,
,![]() ,且曲线
,且曲线![]() 与
与![]() 在
在![]() 处有相同的切线.
处有相同的切线.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求证:![]() 在
在![]() 上恒成立;
上恒成立;
(Ⅲ)当![]() 时,求方程
时,求方程![]() 在区间
在区间![]() 内实根的个数.
内实根的个数.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析;(Ⅲ)2.
;(Ⅱ)证明见解析;(Ⅲ)2.
【解析】
试题分析:
(Ⅰ)函数有相同的切线,则![]() ,
,![]() ,据此计算可得
,据此计算可得![]() ;
;
(Ⅱ)构造函数,令![]() ,原问题等价于
,原问题等价于![]() 在
在![]() 上恒成立,讨论函数的单调性可得
上恒成立,讨论函数的单调性可得![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅲ)构造函数![]() ,其中
,其中![]() ,结合导函数讨论函数的单调性有
,结合导函数讨论函数的单调性有![]()
![]() .构造函数
.构造函数![]() ,则
,则![]() 在
在![]() 内单调递减,
内单调递减,![]() ,据此讨论可得
,据此讨论可得![]() 在区间
在区间![]() 内有两个零点,即方程
内有两个零点,即方程![]() 在区间
在区间![]() 内实根的个数为2.
内实根的个数为2.
试题解析:
(Ⅰ)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,即
,即![]() ,
,
∴![]() .
.
(Ⅱ)证明:设![]() ,
,
![]() .
.
令![]() ,则有
,则有![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
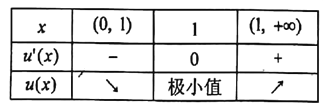
∴![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
(Ⅲ)设![]() ,其中
,其中![]() ,
,
![]() .
.
令![]() ,则有
,则有![]() .
.
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
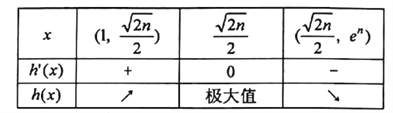
∴![]()
![]() .
.
![]() ,
,
设![]() ,其中
,其中![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 内单调递减,
内单调递减,![]() ,
,
∴![]() ,故
,故![]() ,而
,而![]() .
.
结合函数![]() 的图象,可知
的图象,可知![]() 在区间
在区间![]() 内有两个零点,
内有两个零点,
∴方程![]() 在区间
在区间![]() 内实根的个数为2.
内实根的个数为2.

 名校课堂系列答案
名校课堂系列答案【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整;函数![]() 的解析式为
的解析式为![]() = (直接写出结果即可);
= (直接写出结果即可);
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【题目】甲、乙两台机床生产同一型号零件.记生产的零件的尺寸为![]() (cm),相关行业质检部门规定:若
(cm),相关行业质检部门规定:若![]() ,则该零件为优等品;若
,则该零件为优等品;若![]() ,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
,则该零件为中等品;其余零件为次品.现分别从甲、乙机床生产的零件中各随机抽取50件,经质量检测得到下表数据:
尺寸 |
|
|
|
|
|
|
甲零件频数 | 2 | 3 | 20 | 20 | 4 | 1 |
乙零件频数 | 3 | 5 | 17 | 13 | 8 | 4 |
(Ⅰ)设生产每件产品的利润为:优等品3元,中等品1元,次品亏本1元.若将频率视为概率,试根据样本估计总体的思想,估算甲机床生产一件零件的利润的数学期望;
(Ⅱ)对于这两台机床生产的零件,在排除其它因素影响的情况下,试根据样本估计总体的思想,估计约有多大的把握认为“零件优等与否和所用机床有关”,并说明理由.
参考公式:![]() .
.
参考数据:
![]()
0.25
0.15
0.10
0.05
0.025
0.010
![]()
1.323
2.072
2.706
3.841
5.024
6.635
