题目内容

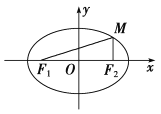
【题目】如图所示，，分别为椭圆的左，右焦点，椭圆上点的横坐标等于右焦点的横坐标，其纵坐标等于短半轴长的，则椭圆的离心率为（ ）

A.B.C.D.

【答案】A

【解析】

设椭圆的长半轴、短半轴、半焦距长分别为a、b、c，可得M（c，b），利用勾股定理与椭圆的定义建立关于a、b、c的等式，化简整理得ba，从而得出ca，即可算出该椭圆的离心率．

设椭圆的长半轴、短半轴、半焦距长分别为a、b、c，

可得焦点为F1（﹣c，0）、F2（c，0），点M的坐标为（c，b），

∵Rt△MF1F2中，F1F2⊥MF2，

∴|F1F2|2+|MF2|2＝|MF1|2，即4c2b2＝|MF1|2，

根据椭圆的定义得|MF1|+|MF2|＝2a，

可得|MF1|2＝（2a﹣|MF2|）2＝（2ab）2，

∴（2ab）2＝4c2b2，整理得4c2＝4a2ab，

可得3（a2﹣c2）＝2ab，所以3b2＝2ab，解得ba，

∴ca，因此可得e，

即该椭圆的离心率等于．

故选：A．

练习册系列答案
相关题目

【题目】已知椭圆C：（a＞b＞0）的离心率为且经过点P（2，）．

（1）求椭圆C的方程；

（2）若椭圆C的左右顶点分别为A，B，过点A斜率为k（k≠0）的直线l交椭圆C于点D，交y轴于点E．是否存在定点Q，对于任意的k（k≠0）都有BD⊥EQ，若存在，求△AQD的面积的最大值；若不存在，说明理由．

【题目】在平面直角坐标系中，动点分别与两个定点，的连线的斜率之积为.

（1）求动点的轨迹的方程；

（2）设过点的直线与轨迹交于，两点，判断直线与以线段为直径的圆的位置关系，并说明理由.

【题目】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．

【题目】设函数.

（Ⅰ）求的单调区间；

（Ⅱ）当时，试判断零点的个数；

（Ⅲ）当时，若对，都有（）成立，求的最大值.

【题目】在如图所示的几何体中，四边形是等腰梯形，，．在梯形中，，且，，平面．

（Ⅰ）求证：．

（II）求四棱锥与三棱锥体积的比值．

【题目】设椭圆的左焦点为，上顶点为.已知椭圆的短轴长为4，离心率为.

（Ⅰ）求椭圆的方程；

（Ⅱ）设点在椭圆上，且异于椭圆的上、下顶点，点为直线与轴的交点，点在轴的负半轴上.若（为原点），且，求直线的斜率.

【题目】若函数y=f（x）在区间D上是增函数，且函数y=在区间D上是减函数，则称函数f（x）是区间D上的“H函数”．对于命题：

①函数f（x）=-x+是区间（0，1）上的“H函数”；

②函数g（x）=是区间（0，1）上的“H函数”．下列判断正确的是（　　）

A. 和均为真命题 B. 为真命题，为假命题

C. 为假命题，为真命题 D. 和均为假命题

【题目】李明自主创业，在网上经营一家水果店，销售的水果中有草莓、京白梨、西瓜、桃，价格依次为60元/盒、65元/盒、80元/盒、90元/盒．为增加销量，李明对这四种水果进行促销：一次购买水果的总价达到120元，顾客就少付x元．每笔订单顾客网上支付成功后，李明会得到支付款的80%．

①当x=10时，顾客一次购买草莓和西瓜各1盒，需要支付__________元；

②在促销活动中，为保证李明每笔订单得到的金额均不低于促销前总价的七折，则x的最大值为__________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网