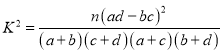题目内容
【题目】已知椭圆C关于x轴、y轴都对称,并且经过两点![]() ,
,
(1)求椭圆C的离心率和焦点坐标;
(2)D是椭圆C上到点A最远的点,椭圆C在点B处的切线l与y轴交于点E,求△BDE外接圆的圆心坐标.
【答案】(1)离心率![]() ,焦点坐标为
,焦点坐标为![]() ;(2)
;(2)![]()
【解析】
(1)根据已知设所求椭圆方程为![]() ,点
,点![]() 坐标代入椭圆方程,求解得到椭圆的标准方程,即可求出离心率和焦点坐标;
坐标代入椭圆方程,求解得到椭圆的标准方程,即可求出离心率和焦点坐标;
(2)设![]() ,利用点
,利用点![]() 在椭圆上,将
在椭圆上,将![]() 表示为关于
表示为关于![]() 的二次函数,求出
的二次函数,求出![]() 最大时
最大时![]() 点坐标;显然椭圆C在点B处的切线l的斜率存在,设出其方程,与椭圆方程联立,利用
点坐标;显然椭圆C在点B处的切线l的斜率存在,设出其方程,与椭圆方程联立,利用![]() ,求出切线
,求出切线![]() 的斜率,进而求出点
的斜率,进而求出点![]() 坐标,利用待定系数法求出△BDE外接圆的一般式方程,即可得出结论.
坐标,利用待定系数法求出△BDE外接圆的一般式方程,即可得出结论.
(1)已知椭圆C关于![]() 轴、
轴、![]() 轴都对称,
轴都对称,
设其方程为![]()
由![]() 在椭圆上,得
在椭圆上,得![]() ,
,
联立解得![]() ,
,![]() ,得椭圆C的方程是
,得椭圆C的方程是![]() .
.
用![]() 依次表示椭圆的长半轴、短半轴、半焦距,
依次表示椭圆的长半轴、短半轴、半焦距,
则![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
所以,椭圆C的离心率![]() ,焦点坐标为
,焦点坐标为![]()
(2)设![]() ,则
,则![]() ,即
,即![]() ,
,
![]()
![]()
![]() .
.
函数![]() 在区间
在区间![]() 上递减,
上递减,
则![]() 取最大时,
取最大时,![]() ,此时
,此时![]() ,
,
所以,椭圆C上到点![]() 最远的点是
最远的点是![]() ;
;
设椭圆C在点![]() 处的切线
处的切线![]() 的方程为
的方程为![]() ,
,
即![]() ,与
,与![]() 联立消去
联立消去![]() 后整理得
后整理得![]() ,
,
判别式![]() ,
,
由相切条件得![]() ,
,![]() ,
,
所以椭圆C在点![]() 处的切线
处的切线![]() 的方程是
的方程是![]() ,
,
令![]() 得
得![]() ,得切线
,得切线![]() 与
与![]() 轴的交点坐标
轴的交点坐标![]() .
.
设![]() 外接圆的方程为
外接圆的方程为![]() ,
,
由三点![]()
![]() 都在圆上,
都在圆上,
得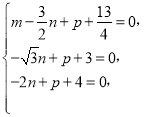 解得
解得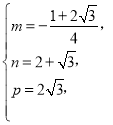
![]() ,
,![]() ,
,
所以![]() 外接圆的圆心坐标是
外接圆的圆心坐标是![]()

 阅读快车系列答案
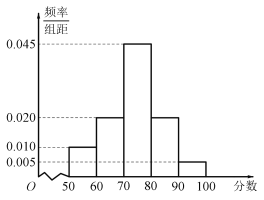
阅读快车系列答案【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
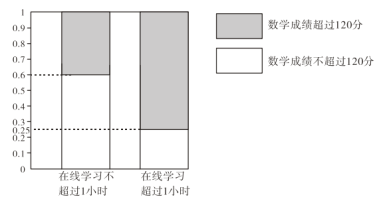
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |