题目内容

15．在各项均为正数的等比数列{an}中，已知a1a5=25，则a3等于（　　）
A．5B．25C．-25D．-5或5

分析 直接由已知结合等差数列的性质求得a3．

解答 解：在等比数列{an}中，由a1a5=25，得${{a}_{3}}^{2}=25$，即a3=±5．
∵an＞0，∴a3=5．
故选：A．

点评 本题考查了等差数列的通项公式，考查等差数列的性质，是基础题．

练习册系列答案
相关题目
5．已知函数f（x）=$\left\{\begin{array}{l}\frac{2}{x}，x≥2\\{（x-1）^3}，0＜x＜2\end{array}\right.$，若关于x的方程f（x）=kx有两个不同的实根，则实数k的取值范围是（　　）
A．$（{0，\frac{1}{2}}）$B．$（{0，\frac{{\sqrt{2}}}{4}}）∪（{\frac{{\sqrt{2}}}{4}，\frac{1}{2}}）$C．$（{\frac{{\sqrt{2}}}{4}，+∞}）$D．$[{\frac{1}{2}，2\sqrt{2}}]$
6．执行如图所示的程序框图，如果输入的x∈[-1，3]，则输出的y属于（　　）
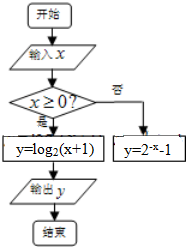
A．[0，2]B．[1，2]C．[0，1]D．[-1，5]
3．已知各项均为正数的数列{an}的前n项和为Sn，且4Sn=an2+2an（n∈N*）．
（1）求a1的值及数列{an}的通项公式；
（2）记数列{$\frac{n+3}{{{a}_{n}}^{3}•{2}^{n}}$}的前n项和为Tn，求证：Tn＜$\frac{9}{32}$（n∈N*）．
10．在△ABC中，角A，B，C所对的边分别为a，b，c，且cos$\frac{A+C}{2}$=$\frac{\sqrt{3}}{3}$．
（1）求cosB的值；
（2）若b=2$\sqrt{2}$，求ac的最大值．
20．已知数列{an}的前n项和Sn=2an-2n+1，若不等式2n2-n-3＜（5-λ）an对?n∈N+恒成立，则整数λ的最大值为4．
7．已知函数f（x）=2$\sqrt{3}sinxcosx+2{cos^2}$x（x∈R）．
（Ⅰ）求函数f（x）的最小正周期及在区间$[{0，\frac{π}{2}}]$上的最大值和最小值；
（Ⅱ）将函数f（x）图象向左平移$\frac{π}{6}$个单位，再向上平移1个单位，得到函数g（x）图象，求g（x）的对称轴方程和对称中心坐标．
4．设函数f（x）=2x-$\frac{3}{x}$+alnx（a∈R），g（x）=3x-$\frac{3}{x}$．
（1）求函数f（x）的单调区间；
（2）若函数g（x）的图象与f（x）的图象有两个交点，求实数a的取值范围．
1．已知点P（2，6）和圆x2+y2+2x-4y-4=0，解答下列问题：
（1）求圆心和半径；
（2）判断点P是否在圆上；
（3）求圆上的点到点P的最长距离和最短距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网