题目内容
16.设数列{an}的前n项和为Sn与an关系是Sn=2-($\frac{1}{2}$)n-1-an,n∈N*.(1)求证:数列{2nan}是等差数列;
(2)设Tn=S1+S2+…+Sn,求Tn.
分析 (1)由数列递推式求得数列首项,取n=n-1得另一递推式,作差后可得数列{2nan}是等差数列;
(2)由(1)求得an,代入Sn=2-($\frac{1}{2}$)n-1-an,分组后利用错位相减法求Tn.
解答 (1)证明:由Sn=2-($\frac{1}{2}$)n-1-an,得a1=2-1-a1,即${a}_{1}=\frac{1}{2}$;
${S}_{n-1}=2-(\frac{1}{2})^{n-2}-{a}_{n-1}$(n≥2),
两式作差得:${a}_{n}=(\frac{1}{2})^{n-2}-{a}_{n}+{a}_{n-1}$,
∴$2{a}_{n}-{a}_{n-1}=(\frac{1}{2})^{n-1}$,即${2}^{n}{a}_{n}-{2}^{n-1}{a}_{n-1}=1$(n≥2),
则数列{2nan}是以1为首项,以1为公差的等差数列;
(2)解:由数列{2nan}是以1为首项,以1为公差的等差数列,
得2nan=1+(n-1)=n,
∴${a}_{n}=\frac{n}{{2}^{n}}$,
则Sn=2-($\frac{1}{2}$)n-1-an=2-$(\frac{1}{2})^{n-1}$-$\frac{n}{{2}^{n}}$=$2-\frac{n+2}{{2}^{n}}$.
∴Tn=S1+S2+…+Sn=2n-($\frac{2}{{2}^{1}}+\frac{3}{{2}^{2}}+\frac{4}{{2}^{3}}+…+\frac{n+2}{{2}^{n}}$),
令Rn=$\frac{2}{{2}^{1}}+\frac{3}{{2}^{2}}+\frac{4}{{2}^{3}}+…+\frac{n+2}{{2}^{n}}$,
则$\frac{1}{2}{R}_{n}=\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+\frac{4}{{2}^{4}}+…+\frac{n+1}{{2}^{n}}+\frac{n+2}{{2}^{n+1}}$,
∴$\frac{1}{2}{R}_{n}=1+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}-\frac{n+2}{{2}^{n+1}}$=$1+\frac{\frac{1}{4}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}-\frac{n+2}{{2}^{n+1}}=\frac{3}{2}-\frac{n+4}{{2}^{n+1}}$,
则${R}_{n}=3-\frac{n+4}{{2}^{n}}$.
∴${T}_{n}=2n-3+\frac{n+4}{{2}^{n}}$.
点评 本题考查了数列递推式,考查了等差关系的确定,训练了错位相减法求数列的和,是中档题.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案(Ⅰ)为便于研究分析,教育专家将A模式称为传统课堂模式,B、C统称为新课堂模式,根据随堂检测结果,把课堂教学效率分为高效和非高效,根据检测结果统计得到如下2×2列联表(单位:节)
| 高效 | 非高效 | 统计 | |
| 新课堂模式 | 60 | 30 | 90 |
| 传统课堂模式 | 40 | 50 | 90 |
| 统计 | 100 | 80 | 180 |
(Ⅱ)教育专家采用分层抽样的方法从收集到的180节课中选出18节课作为样本进行研究,并从样本的B模式和C模式课堂中随机抽取3节课.
①求至少有一节为C模式课堂的概率;
②设随机抽取的3节课中含有C模式课堂的节数为X,求X的分布列和数学期望.
参考临界值表:
| P(K2≧K0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
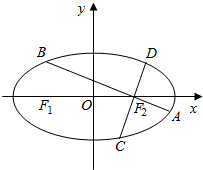 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.