题目内容
【题目】已知函数g(x)=ex , f(x)= ![]() ,f(x)是定义在R上的奇函数.
,f(x)是定义在R上的奇函数.
(1)求a,b的值;
(2)若关于t的方程f(2t2﹣mt)+f(1﹣t2)=0有两个根α、β,且α>0,1<β<2,求实数m的取值范围.
【答案】
(1)解:f(x)是定义在R上的奇函数,
∴f(0)= ![]() ,即a=1.又f(﹣1)=﹣f(1),即
,即a=1.又f(﹣1)=﹣f(1),即 ![]() ,可得b=e.
,可得b=e.
所以f(x)= ![]() .
.
又f(﹣x)= ![]() ,
,
所以a=1,b=e成立
(2)解:f(x)= ![]() ,易得f(x)在R上单调递减.
,易得f(x)在R上单调递减.
方程f(2t2﹣mt)+f(1﹣t2)=0可转化为f(2t2﹣mt)=﹣f(1﹣t2),又函数f(x)是奇函数,则
f(2t2﹣mt)=f(t2﹣1).又函数f(x)在R上单调递减,
所以2t2﹣mt=t2﹣1,即t2﹣mt+1=0.
考虑函数h(t)=t2﹣mt+1,
(i)若α=1或2,则m=2或 ![]() ,易得
,易得 ![]() ,与β∈(1,2)矛盾;
,与β∈(1,2)矛盾;
(ii)若0<α<1或α>2,则h(1)h(2)<0,即(2﹣m)(5﹣2m)<0, ![]() ;
;
(iii)若1<α<2,则只需满足 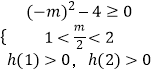 ,
,
由以上(i)、(ii)、(iii)可知 ![]()
【解析】(1)根据奇函数的定义求解;(2)利用奇函数的性质转化为一元二次不等式,借助与一元二次函数的关系进行判断.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目