题目内容
【题目】已知A、B、C、D为圆O上的四点，直线DE为圆O的切线，AC∥DE，AC与BD相交于H点．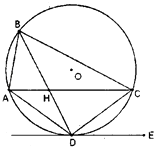
（1）求证：BD平分∠ABC；
（2）若AB=4，AD=6，BD=8，求AH的长．
【答案】
（1）
解：∵AC∥DE，直线DE为圆O的切线，∴D是弧 
的中点，即 
又∠ABD，∠DBC与分别是两弧 
所对的圆周角，故有∠ABD=∠DBC，
所以BD平分∠ABC
（2）
解：∵由图∠CAB=∠CDB且∠ABD=∠DBC
∴△ABH∽△DBC，∴ 
又
∴AD=DC，
∴
∵AB=4，AD=6，BD=8
∴AH=3
【解析】（1）证明BD平分∠ABC可通过证明D是 
的中点，利用相等的弧所对的圆周角相等证明BD是角平分线；（2）由图形知，可先证△ABH∽△DBC，得到 ，再由等弧所对的弦相等，得到AD=DC，从而得到 ，求出AH的长
练习册系列答案
相关题目
【题目】海南大学某餐饮中心为了解新生的饮食习惯，在全校新生中进行了抽样调查，调查结果如下表所示：
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(Ⅰ)根据表中数据，问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”；
(Ⅱ)已知在被调查的北方学生中有5名中文系的学生，其中2名喜欢甜品，现在从这5名学生中随机抽取3人，求至多有1人喜欢甜品的概率．
附：，K2＝
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
