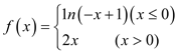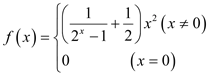题目内容
【题目】已知长方体ABCD﹣A'B'C'D'中,AB=4,AD=3,AA'=2; 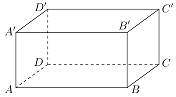
(1)求出异面直线AC'和BD所成角的余弦值;
(2)找出AC'与平面D'DBB'的交点,并说明理由.
【答案】
(1)解:建立如图所示空间直角坐标系,
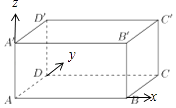
∵AB=4,AD=3,AA'=2;
∴C'(4,3,2),B(4,0,0),D(0,3,0)
则: ![]() =(4,3,2),
=(4,3,2), ![]() =(﹣4,3,0)
=(﹣4,3,0)
异面直线AC'和BD所成角的余弦值为: 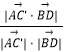 =
= ![]() =
= ![]()
(2)解:连接BD',DB'交于点O,则点O即为AC'与平面D'DBB'的交点,

根据长方体的几何特征可得:
O为长方体ABCD﹣A'B'C'D'外接球的球心,
AC'为长方体ABCD﹣A'B'C'D'外接球的直径,
故O为AC'中点,
又由BD',DB'交于点O,故O在平面D'DBB'上,
故O即为AC'与平面D'DBB'的交点
【解析】(1)建立空间直角坐标系,求出两条线段的方向向量,代入向量夹角公式,可得答案.(2)连接BD',DB'交于点O,则点O即为AC'与平面D'DBB'的交点,根据长方体的性质,可得结论.
【考点精析】认真审题,首先需要了解异面直线及其所成的角(异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系),还要掌握空间中直线与直线之间的位置关系(相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点)的相关知识才是答题的关键.

【题目】海南大学某餐饮中心为了解新生的饮食习惯,在全校新生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(Ⅰ)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(Ⅱ)已知在被调查的北方学生中有5名中文系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:,K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |