题目内容
19．设x∈（0，$\frac{π}{2}$），lgsin2x-lgsinx=lg$\frac{1}{2}$，则tanx等于（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{15}$ | D． | 5 |
分析 根据对数函数的运算性质和二倍角的正弦公式得到cosx=$\frac{1}{4}$，再由同角三角函数的基本关系，得到答案．
解答 解：∵lgsin2x-lgsinx=lg$\frac{sin2x}{sinx}$=lg（2cosx）=lg$\frac{1}{2}$，
∴2cosx=$\frac{1}{2}$，
∴cosx=$\frac{1}{4}$，
∵x∈（0，$\frac{π}{2}$），
∴sinx=$\sqrt{1-{cos}^{2}x}$=$\frac{\sqrt{15}}{4}$，
∴tanx=$\frac{sinx}{cosx}$=$\sqrt{15}$，
故选：C
点评 本题考查了二倍角的正弦，同角三角函数的基本关系，对数的运算性质，属于中档题，牢记sin2α=2sinα•cosα是解题的突破口．
练习册系列答案
相关题目
9．设数列Sn是等差数列{an}的前n项和，若a3=5，a8=11，则S10=（ ）
| A． | 90 | B． | 80 | C． | 100 | D． | 120 |
10．若（1-2x）11=a0+a1x+a2x2+…+a11x11，则a2+a3+…+a11等于（ ）
| A． | 20 | B． | 16 | C． | -18 | D． | -17 |
7．
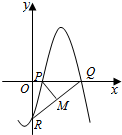如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）与坐标轴的三个交点P、Q、R满足P（1，0），M（2，-2）为线段QR的中点，则A=（ ）
如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤$\frac{π}{2}$）与坐标轴的三个交点P、Q、R满足P（1，0），M（2，-2）为线段QR的中点，则A=（ ）| A． | 2$\sqrt{3}$ | B． | $\frac{7\sqrt{3}}{3}$ | C． | $\frac{8\sqrt{3}}{3}$ | D． | 4$\sqrt{3}$ |
如图，在直三棱柱ABC-A1B1C1中，已知点D为棱BC中点．