题目内容
18.已知一段演绎推理:“因为指数函数y=ax是增函数,而$y={(\frac{1}{2})^x}$是指数函数,所以$y={(\frac{1}{2})^x}$是增函数”,则这段推理的( )| A. | 大前提错误 | B. | 小前提错误 | C. | 结论正确 | D. | 推理形式错误 |
分析 分析该演绎推理的大前提、小前提和结论,结合指数函数的图象和性质判断正误,可以得出正确的答案.
解答 解:该演绎推理的大前提是:指数函数y=ax是增函数,
小前提是:y=($\frac{1}{2}$)x是指数函数,
结论是:y=($\frac{1}{2}$)x是增函数.
其中,大前提是错误的,因为0<a<1时,函数y=ax是减函数,致使得出的结论错误.
故选:A
点评 本题考查了演绎推理的应用问题,解题时应根据演绎推理的三段论是什么,进行逐一判定,得出正确的结论,是基础题.

练习册系列答案
相关题目
9.设数列Sn是等差数列{an}的前n项和,若a3=5,a8=11,则S10=( )
| A. | 90 | B. | 80 | C. | 100 | D. | 120 |
6.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为( )
| A. | 120° | B. | 150° | C. | 180° | D. | 240° |
3.复数z=$\frac{5i}{1-2i}$(i为虚数单位)的共轭复数$\overline{z}$等于( )
| A. | -1-2i | B. | 1+2i | C. | 2-i | D. | -2-i |
10.若(1-2x)11=a0+a1x+a2x2+…+a11x11,则a2+a3+…+a11等于( )
| A. | 20 | B. | 16 | C. | -18 | D. | -17 |
7.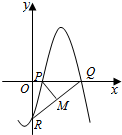 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
 如图,在直三棱柱ABC-A1B1C1中,已知点D为棱BC中点.
如图,在直三棱柱ABC-A1B1C1中,已知点D为棱BC中点.