题目内容
18．七人排成两排，前排3人，后排4人，若甲必须在前排，乙必须在后排，有1440种不同排法．分析 首先要分三步完成：①固定甲、乙两人，剩下7-2=5人，从5人中选2人站前排；②前排3人进行任意排列；③后排4人任意排列；再进一步利用乘法原理解决问题．
解答 解：从5人中任选2人站前排有${C}_{5}^{2}$=5×4÷2=10种方法；
前排3人（包括甲）任意排列有${A}_{3}^{3}$=3×2×1=6种方法；
后排4人（包括乙）任意排列有${A}_{4}^{4}$=4×3×2×1=24种方法；
所以一共有10×6×24=1440种方法；
故答案为：1440．
点评 解答此题的关键首先分步，然后利用乘法原理解决问题．
练习册系列答案
相关题目
3．已知等比数列{an}中，an=2×3n-1，则由此数列的偶数项所组成的新数列的前n项和Sn的值为（ ）
| A． | 3n-1 | B． | 3（3n-1） | C． | $\frac{{{9^n}-1}}{4}$ | D． | $\frac{{3（{9^n}-1）}}{4}$ |
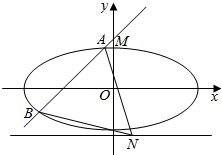已知点P（2，$\frac{\sqrt{5}}{5}$）是椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上一点，且点P在x轴上的射影恰好是椭圆C的焦点．
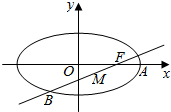椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）斜率为$\frac{b}{a}$的直线与椭圆C交于A、B两点（如图），AB中点为M，MA中点时椭圆C的右焦点F，求椭圆C的离心率e．