Question

【题目】已知函数f（x）=log2（x+a）．

（Ⅰ）当a=1时，若f（x）+f（x-1）＞0成立，求x的取值范围；

（Ⅱ）若定义在R上奇函数g（x）满足g（x+2）=-g（x），且当0≤x≤1时，g（x）=f（x），求g（x）在[-3，-1]上的解析式，并写出g（x）在[-3，3]上的单调区间（不必证明）；

（Ⅲ）对于（Ⅱ）中的g（x），若关于x的不等式g（）≥g（-）在R上恒成立，求实数t的取值范围．

Answer 1

【答案】（I）；（II）见解析；（III）.

【解析】

（Ⅰ）当时，可化为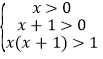，解不等式组可得答案

（II）根据已知可得，在结合条件求得的解析式，进而分析出在上的单调区间

（III）关于的不等式在上恒成立，即，分类讨论后，综合讨论结果，可得答案

解：（Ⅰ）当a=1时，f（x）=log2（x+1）．

∴f（x-1）=log2x，

∴f（x）+f（x-1）=log2（x+1）+log2x=log2[x（x+1）]，

若f（x）+f（x-1）＞0，则，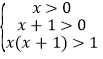

解得：x∈（，+∞），

即x的取值范围为（，+∞）；

（Ⅱ）∵函数g（x）是定义在R上奇函数，

故g（0）=0，

又∵当0≤x≤1时，g（x）=f（x）=log2（x+a）．

故a=1，

当x∈[-2，-1]时，x+2∈[0，1]，

∴g（x）=-g（x+2）=-log2（x+3）．

当x∈[-3，-2]时，x+2∈[-1，0]，-（x+2）∈[0，1]，

∴g（x）=-g（x+2）=g[-（x+2）]=log2[-（x+2）+1]=log2（-x-1）．

故g（x）=，

g（x）在[-3，-1]和[1，3]上递减，在[-1，1]上递增；

（III）记u==-+，

当t+1≥0时，u∈（-，-+）=（-，），

由g（）≥g（-）在R上恒成立可得：（-，）[，]，

解得：t∈[-1，20]．

当t+1＜0时，u∈（-+，-）=（，-），

由g（）≥g（-）在R上恒成立可得：（，-）[.]，

解得：t∈[-4，-1）．

综上所述实数t的取值范围为[-4，20]．