题目内容
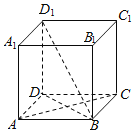
【题目】如图，在正方体ABCD-A1B1C1D1中．
（I）求证：AC⊥BD1；
（Ⅱ）是否存在直线与直线AA1，CC1，BD1都相交？若存在，请你在图中画出两条满足条件的直线（不必说明画法及理由）；若不存在，请说明理由．
【答案】（I）详见解析；（II）存在，图形见解析.
【解析】
（Ⅰ）连结
，推导出
，
，由此能证明
（Ⅱ）作出满足条件的直线一定在平面
中，且过
的中点并与直线
，
相交
（Ⅰ）证明：如图，连结BD
∵正方体ABCD-A1B1C1D1，
∴D1D⊥平面ABCD．
∵AC平面ABCD，∴D1D⊥AC．
∵四边形ABCD是正方形，∴AC⊥BD．
∵BD∩D1D=D，∴AC⊥平面BDD1．
∵BD1平面BDD1，∴AC⊥BD1．
（Ⅱ）存在．答案不唯一，
作出满足条件的直线一定在平面ACC1A1中，
且过BD1的中点并与直线A1A，C1C相交．
【题目】甲，乙，丙三位学生独立地解同一道题，甲做对的概率为 
，乙，丙做对的概率分别为m，n（m＞n），且三位学生是否做对相互独立．记ξ为这三位学生中做对该题的人数，其分布列为：
ξ | 0 | 1 | 2 | 3 |
P |
| a | b |
|
（1）求至少有一位学生做对该题的概率；
（2）求m，n的值；
（3）求ξ的数学期望．
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：
年 份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程；
(2)利用(1)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
附：回归直线的斜率和截距的最小二乘估计公式分别为：
＝
，
＝
－
．
【题目】为了调查每天人们使用手机的时间，我校某课外兴趣小组在天府广场随机采访男性、女性用户各50 名，其中每天玩手机超过6小时的用户列为“手机控”，否则称其为“非手机控”，调查结果如下：
手机控 | 非手机控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据以上数据，能否有60%的把握认为“手机控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取5人中“手机控”和“非手机控”的人数；
（3）从（2）中抽取的5人中再随机抽取3人，记这3人中“手机控”的人数为X，试求X的分布列与数学期望． 参考公式： 
．
参考数据：
P（K2≥k0） | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.456[ | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
