题目内容
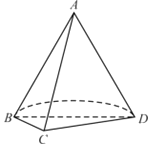
【题目】如图,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() .
.![]() 为
为![]() 的中点,
的中点, ![]() .
.
(1)求证: ![]() ;
;
(2)若![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明过程详见解析;(2)![]() .
.
【解析】试题(1)连结![]() ,则
,则![]() ,从而得到
,从而得到![]() ,进而得到
,进而得到![]() ,由此能证明
,由此能证明![]() ;(2)由(1)得
;(2)由(1)得![]() .不妨设
.不妨设![]() ,
, ![]() ,取
,取![]() 的中点为
的中点为![]() ,建立坐标系,求出平面
,建立坐标系,求出平面![]() 的法向量、平面
的法向量、平面![]() 的法向量,利用向量的夹角公式,利用向量法即可.试题解析:(1)证明:连结
的法向量,利用向量的夹角公式,利用向量法即可.试题解析:(1)证明:连结![]() ,因
,因![]() ,
, ![]() 是
是![]() 的中点,故
的中点,故![]() .
.
又因平面![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,
于是![]() .又
.又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() ,又因
,又因![]() ,故
,故![]() 平面
平面![]() ,
,
所以![]() .
.
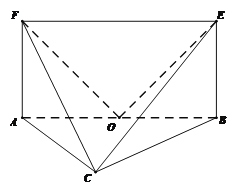
(2)由(1),得![]() ,不妨设
,不妨设![]() ,则
,则![]() ,取
,取![]() 的中点
的中点![]() ,以
,以![]() 为原点,
为原点, ![]() 所在的直线分别为
所在的直线分别为![]() 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则![]()
从而![]() .
.
设平面![]() 的法向量
的法向量![]() ,由
,由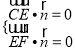 ,得
,得![]() ,
,
同理可求得平面![]() 的法向量
的法向量![]() ,设
,设![]() 的夹角为
的夹角为![]() ,则
,则![]() ,
,
由于二面角![]() 为钝二面角,则余弦值为
为钝二面角,则余弦值为![]() .
.

练习册系列答案
相关题目
【题目】细叶青萎藤又称海风藤,俗称穿山龙,属木质藤本植物,是我国常用大宗中药材,以根茎入药,具有舒筋活血、祛风止痛、止咳平喘、强身健体等医疗保健功效.通过研究光照、温度和沙藏时间对细叶青萎藤种子萌发的影响,结果表明,细叶青萎藤种子发芽率和发芽指数均随着沙藏时间的延长而提高.
下表给岀了2019年种植的一批试验细叶青萎藤种子6组不同沙藏时间发芽的粒数.经计算:
沙藏时间 | 22 | 23 | 25 | 27 | 29 | 30 |
发芽数 | 8 | 11 | 20 | 30 | 59 | 70 |
![]() ,
,![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() 分别为试验数据中的天数和发芽粒数,
分别为试验数据中的天数和发芽粒数,![]() .
.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到0.01);
都精确到0.01);
(2)在题中的6组发芽的粒数不大于30的组数中,任意抽岀两组,则这两组数据中至少有一组满足“![]() ”的概率是多少?
”的概率是多少?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: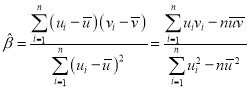 ,
,![]() .
.