题目内容
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() )的上顶点为
)的上顶点为![]() ,圆
,圆![]() 经过点
经过点![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交圆
交圆![]() 于另一点
于另一点![]() .若△PQN的面积为3,求直线
.若△PQN的面积为3,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)依据题意可得:![]() ,由圆
,由圆![]() 经过点
经过点![]() 可得:
可得:![]() ,问题得解。
,问题得解。
(2)当![]() 的斜率为0时,检验得不合题意,可设设直线
的斜率为0时,检验得不合题意,可设设直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程可得
,联立直线与椭圆方程可得![]() ,设
,设![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,由弦长公式可得:
,由弦长公式可得:![]() ,由△PQN的面积为3列方程可得:
,由△PQN的面积为3列方程可得: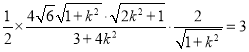 ,即可求得:
,即可求得:![]() ,问题得解。
,问题得解。
(1)因为椭圆![]() 的上顶点为
的上顶点为![]() ,所以
,所以![]() ,又圆
,又圆![]() 经过点
经过点![]() ,
,
所以![]() . 所以椭圆
. 所以椭圆![]() 的方程为
的方程为![]() .
.
(2)若![]() 的斜率为0,则
的斜率为0,则![]() ,
,![]() ,
,
所以△PQN的面积为![]() ,不合题意,所以直线
,不合题意,所以直线![]() 的斜率不为0.
的斜率不为0.
设直线![]() 的方程为
的方程为![]() ,由
,由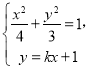 消
消![]() 得
得![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
所以![]()
![]() .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,所以
,所以![]() .
.
所以△PQN的面积![]()
![]() ,
,
解得![]() ,即直线
,即直线![]() 的斜率为
的斜率为![]() .
.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
【题目】有5个匣子,每个匣子有一把钥匙,并且钥匙不能通用.如果随意在每一个匣内放入一把钥匙,然后把匣子全都锁上.现在允许砸开一个匣子,使得能相继用钥匙打开其余4个匣子,那么钥匙的放法有______种.
【题目】随着西部大开发的深入,西南地区的大学越来越受到广大考生的青睐,下表是西南地区某大学近五年的录取平均分高于省一本线分值对比表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
录取平均分高于省一本线分值 | 28 | 34 | 41 | 47 | 50 |
(1)根据上表数据可知,![]() 与
与![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)假设2020年该省一本线为520分,利用(1)中求出的回归方程预测2020年该大学录取平均分.
参考公式: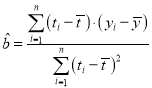 ,
,![]()