题目内容
7.已知椭圆的中心在原点,左焦点为${F_1}(-\sqrt{3},0)$,右顶点为D(2,0),设点A(1,$\frac{1}{2}$).(1)求椭圆的标准方程
(2)若一过原点的直线与椭圆交于点B,C,求△ABC的面积最大值.
分析 (1)由左焦点为${F_1}(-\sqrt{3},0)$,右顶点为D(2,0),得到椭圆的半长轴a,半焦距c,再求得半短轴b,最后由椭圆的焦点在x轴上求得方程.
(2)当BC垂直于x轴时,BC=2,S△ABC=1;当BC不垂直于x轴时,设该直线方程为y=kx,代入椭圆方程,求得B,C的坐标,进而求得弦长|BC|,再求原点到直线的距离,从而可得三角形面积模型,再用基本不等式求其最值.
解答 解:(1)由已知得椭圆的半长轴a=2,半焦距c=$\sqrt{3}$,则半短轴b=1.
又椭圆的焦点在x轴上,
∴椭圆的标准方程$\frac{{x}^{2}}{4}+{y}^{2}=1$
(2)当BC垂直于x轴时,BC=2,S△ABC=1
当BC不垂直于x轴时,设该直线方程为y=kx,代入$\frac{{x}^{2}}{4}+{y}^{2}=1$
解得B($\frac{2}{\sqrt{4{k}^{2}+1}},\frac{2k}{\sqrt{4{k}^{2}+1}}$),C($-\frac{2}{\sqrt{4{k}^{2}+1}},-\frac{2k}{\sqrt{4{k}^{2}+1}}$)
则|BC|=4$\frac{\sqrt{1+{k}^{2}}}{\sqrt{1+4{k}^{2}}}$,又点A到直线BC的距离d=$\frac{|k-\frac{1}{2}|}{\sqrt{1+{k}^{2}}}$
∴△ABC的面积S△ABC=$\frac{1}{2}|BC|•d=\frac{|2k-1|}{\sqrt{1+4{k}^{2}}}$
于是${S}_{△ABC}=\sqrt{\frac{4{k}^{2}-4k+1}{4{k}^{2}+1}}=\sqrt{1-\frac{4k}{4{k}^{2}+1}}$
要使△ABC面积的最大值,则k<0
由$\frac{4k}{4{k}^{2}+1}≥-1$,得S△ABC$≤\sqrt{2}$,其中,当k=-$\frac{1}{2}$时,等号成立
∴S△ABC的最大值是$\sqrt{2}$
点评 本题的考点是直线与圆锥曲线的综合问题,主要考查椭圆的几何性质,考查椭圆的标准方程,考查直线与椭圆的位置关系,求三角形面积的最值,关键是构建模型,利用基本不等式求解.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 16 | B. | 18 | C. | 22 | D. | 20 |
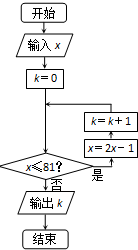
| A. | (21,41) | B. | [21,41] | C. | (21,41] | D. | [21,41) |
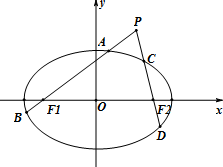 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.