题目内容
16.已知直线AB中,A(1,0),B(2,$\sqrt{3}$)(1)求直线AB的倾斜角;
(2)若直线AD与直线AB垂直,求直线AD的方程,并化为一般式.
分析 (1)先求出直线AB的斜率,即可求直线AB的倾斜角;
(2)根据直线垂直的斜率关系求出直线斜率,即可得到结论.
解答 解:(1)AB的斜率k=$\frac{\sqrt{3}-0}{2-1}=\sqrt{3}$,
由tanα=$\sqrt{3}$,解得α=$\frac{π}{3}$,
即直线AB的倾斜角α=$\frac{π}{3}$;
(2)若直线AD与直线AB垂直,
则直线AD的斜率k=$-\frac{1}{\sqrt{3}}$=$-\frac{\sqrt{3}}{3}$,
则AD的方程为y-0=$-\frac{\sqrt{3}}{3}$(x-1),
即$\sqrt{3}x+3y-\sqrt{3}=0$,
即x+$\sqrt{3}y$-1=0.
点评 本题主要考查直线斜率的计算以及直线方程的求解,根据直线垂直对应斜率之间的关系是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
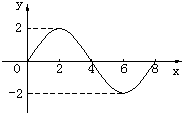
14.下图是函数f(x)=Asinωx(A>0,ω>0)一个周期的图象,则f(1)+f(2)+f(3)+f(4)+f(5)+f(6)的值等于( )

| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
11.下列数列中,是等差数列的是( )
| A. | -1,0,-1,0,… | B. | 1,11,111,1111,… | C. | 1,5,9,13,… | D. | 1,2,4,8,… |
1.已知a>0,若不等式loga+3x-loga+1x+5≤n+$\frac{6}{n}$对任意n∈N*恒成立,则实数x的取值范围是( )
| A. | [1,+∞) | B. | (0,1] | C. | [3,+∞) | D. | [1,3] |