题目内容
【题目】平面直角坐标系![]() 中,椭圆C:
中,椭圆C:![]() 的离心率是
的离心率是![]() ,抛物线E:
,抛物线E:![]() 的焦点F是C的一个顶点.
的焦点F是C的一个顶点.
(Ⅰ)求椭圆C的方程;
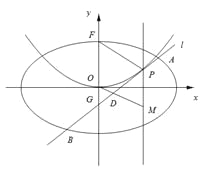
(Ⅱ)设P是E上的动点,且位于第一象限,E在点P处的切线![]() 与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
与C交与不同的两点A,B,线段AB的中点为D,直线OD与过P且垂直于x轴的直线交于点M.
(ⅰ)求证:点M在定直线上;
(ⅱ)直线![]() 与y轴交于点G,记△
与y轴交于点G,记△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点P的坐标.
的最大值及取得最大值时点P的坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)(Ⅰ)见解析;(Ⅱ)
;(Ⅱ)(Ⅰ)见解析;(Ⅱ)![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
【解析】
试题分析:(Ⅰ)根据椭圆的离心率和焦点求方程;(Ⅱ)(Ⅰ)由点P的坐标和斜率设出直线l的方程和抛物线联立,进而判断点M在定直线上;(Ⅱ)分别列出![]() ,
,![]() 面积的表达式,根据二次函数求最值和此时点P的坐标.
面积的表达式,根据二次函数求最值和此时点P的坐标.
试题解析:
(Ⅰ)由题意知![]() ,可得:
,可得:![]() .
.
因为抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)(Ⅰ)设![]() ,由
,由![]() 可得
可得![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
因此直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
设![]() ,联立方程
,联立方程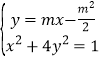
得![]() ,
,
由![]() ,得
,得![]() 且
且![]() ,
,
因此![]() ,
,
将其代入![]() 得
得![]() ,
,
因为![]() ,所以直线
,所以直线![]() 方程为
方程为![]() .
.
联立方程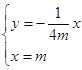 ,得点
,得点![]() 的纵坐标为
的纵坐标为![]() ,
,
即点![]() 在定直线
在定直线![]() 上.
上.
(Ⅱ)由(Ⅰ)知直线![]() 方程为
方程为![]() ,
,
令![]() 得
得![]() ,所以
,所以![]() ,
,
又![]()
![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() ,
,
令![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ,满足
,满足![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,因此
,因此![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() .
.

练习册系列答案
相关题目