题目内容
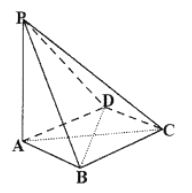
【题目】已知![]() 是边长为2的正三角形,在
是边长为2的正三角形,在![]() 内任取一点,则该点落在
内任取一点,则该点落在![]() 内切圆内的概率是( )
内切圆内的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:根据题意求出△ABC内切圆的面积与三角形的面积比即可.
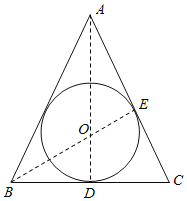
详解:如图所示,△ABC是边长为2的正三角形,
则AD=![]() ,OD=
,OD=![]() ,
,
∴△ABC内切圆的半径为r=![]() ,
,
所求的概率是P=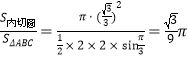 .
.
故答案为:D
点睛:(1)本题主要考查几何概型的计算和解三角形,意在考查学生对这些基础知识的掌握水平.(2)几何概型的解题步骤:首先是判断事件是一维问题还是二维、三维问题(事件的结果与一个变量有关就是一维的问题,与两个变量有关就是二维的问题,与三个变量有关就是三维的问题);接着,如果是一维的问题,先确定试验的全部结果和事件![]() 构成的区域长度(角度、弧长等),最后代公式
构成的区域长度(角度、弧长等),最后代公式![]() ;如果是二维、三维的问题,先设出二维或三维变量,再列出试验的全部结果和事件
;如果是二维、三维的问题,先设出二维或三维变量,再列出试验的全部结果和事件![]() 分别满足的约束条件,作出两个区域,最后计算两个区域的面积或体积代公式.
分别满足的约束条件,作出两个区域,最后计算两个区域的面积或体积代公式.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过长期观测,![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)若船舶航行时,水深至少要![]() 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?