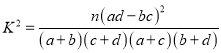ĢāÄæÄŚČŻ
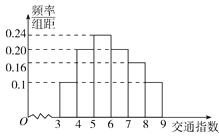
”¾ĢāÄæ”æÄ³Ć½ĢåĪŖĮĖ½āijµŲĒų“óѧɜĶķÉĻ·ÅѧŗóŹ¹ÓĆŹÖ»śÉĻĶųĒéæö£¬Ė껜³éČ”ĮĖ100Ćū“óѧɜ½ųŠŠµ÷²é£®ČēĶ¼ŹĒøł¾Żµ÷²é½į¹ū»ęÖʵÄѧɜĆæĶķŹ¹ÓĆŹÖ»śÉĻĶųĘ½¾łĖłÓĆŹ±¼äµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£®½«Ź±¼ä²»µĶÓŚ40·ÖÖÓµÄѧɜ³ĘĪŖ”°ŹÖ»śĆŌ”±£® 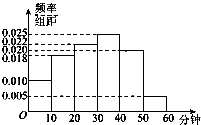
£Ø1£©Ńł±¾ÖŠ”°ŹÖ»śĆŌ”±ÓŠ¶ąÉŁČĖ£æ
£Ø2£©øł¾ŻŅŃÖŖĢõ¼žĶź³ÉĻĀĆęµÄ2”Į2ĮŠĮŖ±ķ£¬²¢¾Ż“Ė׏ĮĻÅŠ¶ĻŹĒ·ńÓŠ95%µÄ°ŃĪÕČĻĪŖ”°ŹÖ»śĆŌ”±ÓėŠŌ±šÓŠ¹Ų£æ
£Ø3£©½«ÉĻŹöµ÷²éĖłµĆµ½µÄʵĀŹŹÓĪŖøÅĀŹ£®ĻÖŌŚ“ÓøƵŲĒų“óĮæ“óѧ ÉśÖŠ£¬²ÉÓĆĖ껜³éŃł·½·ØĆæ“Ī³éČ”1Ćū“óѧɜ£¬³éČ”3“Ī£¬¾µ÷²éŅ»Ćū”°ŹÖ»śĆŌ”±±Č”°·ĒŹÖ»śĆŌ”±ĆæŌĀµÄ»°·ŃĘ½¾ł¶ą40ŌŖ£¬¼Ē±»³éČ”µÄ3Ćū“óѧɜ֊µÄ”°ŹÖ»śĆŌ”±ČĖŹżĪŖX£¬ĒŅÉč3ČĖĆæŌĀµÄ×Ü»°·Ń±Č”°·ĒŹÖ»śĆŌ”±¹²¶ą³öYŌŖ£¬ČōĆæ“Ī³éČ”µÄ½į¹ūŹĒĻą»„¶ĄĮ¢µÄ£¬ĒóXµÄ·Ö²¼ĮŠŗĶYµÄĘŚĶūEY
”¾“š°ø”æ
£Ø1£©½ā£ŗÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼æÉÖŖ£¬
ŌŚ³éČ”µÄ100ČĖÖŠ£¬”°ŹÖ»śĆŌ”±ÓŠ£ŗ
100”Į£Ø0.2+0.05£©=25ČĖ
£Ø2£©½ā£ŗ“Ó¶ų2”Į2ĮŠĮŖ±ķČēĻĀ£ŗ
·ĒŹÖ»śĆŌ | ŹÖ»śĆŌ | ŗĻ¼Ę | |
ÄŠ | 30 | 15 | 45 |
Å® | 45 | 10 | 55 |
ŗĻ¼Ę | 75 | 25 | 100 |
¼ŁÉčH0£ŗ”°ŹÖ»śĆŌ”±ÓėŠŌ±šĆ»ÓŠ¹ŲĻµ£®
½«2”Į2ĮŠĮŖ±ķÖŠµÄŹż¾Ż“śČė¹«Ź½£¬¼ĘĖćµĆ£ŗ
![]() £®
£®
µ±H0³ÉĮ¢Ź±£¬P£ØK2”Ż3.841£©”Ö0.05£®
”ą3.030£¼3.841£¬ĖłŅŌƻӊ95%°ŃĪÕČĻĪŖ”°ŹÖ»śĆŌ”±ÓėŠŌ±šÓŠ¹Ų£®
£Ø3£©½ā£ŗÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÖŖ£¬³éµ½”°ŹÖ»śĆŌ”±µÄʵĀŹĪŖ0.25£¬
½«ĘµĀŹŹÓĪŖøÅĀŹ£¬¼““Ó“óѧɜ֊³éČ”Ņ»Ćū”°ŹÖ»śĆŌ”±µÄøÅĀŹĪŖ ![]() £®
£®
ÓÉĢāŅāÖŖ£¬X”«B£Ø3£¬ ![]() £©£®ĒŅY=40X
£©£®ĒŅY=40X
”ąXµÄ·Ö²¼ĮŠĪŖ£ŗ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
£¬ ![]()
”¾½āĪö”æ£Ø1£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÄÜĒó³öŌŚ³éČ”µÄ100ČĖÖŠ£¬”°ŹÖ»śĆŌ”±µÄČĖŹż£®£Ø2£©Ēó³ö2”Į2ĮŠĮŖ±ķ£¬¼ŁÉčH0£ŗ”°ŹÖ»śĆŌ”±ÓėŠŌ±šĆ»ÓŠ¹ŲĻµ£¬Ēó³öK2= ![]() £¼3.841£¬“Ó¶ųµĆµ½Ć»ÓŠ95%°ŃĪÕČĻĪŖ”°ŹÖ»śĆŌ”±ÓėŠŌ±šÓŠ¹Ų£®£Ø3£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÖŖ£¬³éµ½”°ŹÖ»śĆŌ”±µÄʵĀŹĪŖ0.25£¬½«ĘµĀŹŹÓĪŖøÅĀŹ£¬¼““Ó“óѧɜ֊³éČ”Ņ»Ćū”°ŹÖ»śĆŌ”±µÄøÅĀŹĪŖ
£¼3.841£¬“Ó¶ųµĆµ½Ć»ÓŠ95%°ŃĪÕČĻĪŖ”°ŹÖ»śĆŌ”±ÓėŠŌ±šÓŠ¹Ų£®£Ø3£©ÓÉʵĀŹ·Ö²¼Ö±·½Ķ¼ÖŖ£¬³éµ½”°ŹÖ»śĆŌ”±µÄʵĀŹĪŖ0.25£¬½«ĘµĀŹŹÓĪŖøÅĀŹ£¬¼““Ó“óѧɜ֊³éČ”Ņ»Ćū”°ŹÖ»śĆŌ”±µÄøÅĀŹĪŖ ![]() £®ÓÉĢāŅāÖŖ£¬X”«B£Ø3£¬
£®ÓÉĢāŅāÖŖ£¬X”«B£Ø3£¬ ![]() £©£®ĒŅY=40X£¬ÓÉ“ĖÄÜĒó³öXµÄ·Ö²¼ĮŠŗĶYµÄĘŚĶūEY£®
£©£®ĒŅY=40X£¬ÓÉ“ĖÄÜĒó³öXµÄ·Ö²¼ĮŠŗĶYµÄĘŚĶūEY£®

 ÅąÓÅæŚĖćĢāæØĻµĮŠ“š°ø
ÅąÓÅæŚĖćĢāæØĻµĮŠ“š°ø æŖŠÄæŚĖćĢāæØĻµĮŠ“š°ø
æŖŠÄæŚĖćĢāæØĻµĮŠ“š°ø æŚĖćĢāæØŗÓ±±ÉŁÄź¶łĶƳö°ęÉēĻµĮŠ“š°ø
æŚĖćĢāæØŗÓ±±ÉŁÄź¶łĶƳö°ęÉēĻµĮŠ“š°ø A¼Ó½šĢā ĻµĮŠ“š°ø
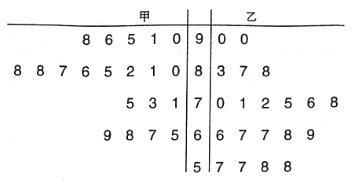
A¼Ó½šĢā ĻµĮŠ“š°ø”¾ĢāÄæ”æĪŖµ÷²éøßÖŠÉśµÄŹżŃ§³É¼ØÓėѧɜ×ŌÖ÷ѧĻ°Ź±¼äÖ®¼äµÄĻą¹Ų¹ŲĻµ£¬³¤æ¤ÖŠŃ§ŹżŃ§½ĢŹ¦¶ŌŠĀČėѧµÄ45Ćūѧɜ½ųŠŠĮĖøś×Łµ÷²é£¬ĘäÖŠĆæÖÜ×ŌÖ÷×öŹżŃ§ĢāµÄŹ±¼ä²»ÉŁÓŚ15Š”Ź±µÄÓŠ19ČĖ£¬ÓąĻĀµÄČĖÖŠ£¬ŌŚøßČżÄ£Äāæ¼ŹŌÖŠŹżŃ§Ę½¾ł³É¼Ø²»×ć120·ÖµÄÕ¼![]() £¬Ķ³¼Ę³É¼Øŗó£¬µĆµ½ČēĻĀµÄ
£¬Ķ³¼Ę³É¼Øŗó£¬µĆµ½ČēĻĀµÄ![]() ĮŠĮŖ±ķ£ŗ
ĮŠĮŖ±ķ£ŗ
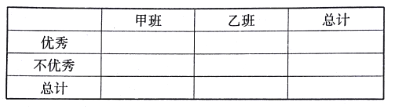
·ÖŹż“óÓŚµČÓŚ120·Ö | ·ÖŹż²»×ć120·Ö | ŗĻ¼Ę | |
ÖÜ×öĢāŹ±¼ä²»ÉŁÓŚ15Š”Ź± | 4 | 19 | |
ÖÜ×öĢāŹ±¼ä²»×ć15Š”Ź± | |||
ŗĻ¼Ę | 45 |
£Ø1£©ĒėĶź³ÉÉĻĆęµÄ![]() ĮŠĮŖ±ķ£¬²¢ÅŠ¶ĻÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.01µÄĒ°ĢįĻĀČĻĪŖ”°øßÖŠÉśµÄŹżŃ§³É¼ØÓėѧɜ×ŌÖ÷ѧĻ°Ź±¼äÓŠ¹Ų”±£»
ĮŠĮŖ±ķ£¬²¢ÅŠ¶ĻÄÜ·ńŌŚ·ø“ķĪóµÄøÅĀŹ²»³¬¹ż0.01µÄĒ°ĢįĻĀČĻĪŖ”°øßÖŠÉśµÄŹżŃ§³É¼ØÓėѧɜ×ŌÖ÷ѧĻ°Ź±¼äÓŠ¹Ų”±£»
£Ø2£©£Ø¢”£©°“ÕÕ·Ö²ć³éŃłµÄ·½·Ø£¬ŌŚÉĻŹöŃł±¾ÖŠ£¬“Ó·ÖŹż“óÓŚµČÓŚ120·ÖŗĶ·ÖŹż²»×ć120·ÖĮ½×éѧɜ֊³éČ”9Ćūѧɜ£¬Éč³éµ½µÄ²»×ć120·ÖĒŅÖÜ×öĢāŹ±¼ä²»×ć15Š”Ź±µÄČĖŹżŹĒ![]() £¬Ēó
£¬Ēó![]() µÄ·Ö²¼ĮŠ£ØøÅĀŹÓĆ×éŗĻŹżĖćŹ½±ķŹ¾£©£»
µÄ·Ö²¼ĮŠ£ØøÅĀŹÓĆ×éŗĻŹżĖćŹ½±ķŹ¾£©£»
£Ø¢¢£©Čō½«ĘµĀŹŹÓĪŖøÅĀŹ£¬“ÓČ«Š£“óÓŚµČÓŚ120·ÖµÄѧɜ֊Ė껜³éČ”20ČĖ£¬ĒóÕāŠ©ČĖÖŠÖÜ×öĢāŹ±¼ä²»ÉŁÓŚ15Š”Ź±µÄČĖŹżµÄĘŚĶūŗĶ·½²ī.
|
|
|
|
|
|
|
|
ø½£ŗ