题目内容
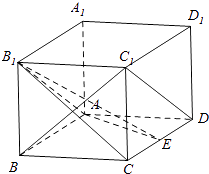
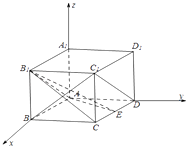
【题目】如图，在长方体ABCD﹣A1B1C1D1中，AA1=AD=1，E为CD中点．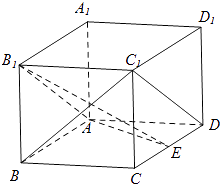 
（1）求证：C1D∥平面AB1E；
（2）求证：BC1⊥B1E；
（3）若AB= 
，求二面角E﹣AB1﹣B的正切值．
【答案】
（1）证明：由长方体性质可知，B1C1∥BC，BC∥AD，且三者都相等
∴四边形B1C1DA是平行四边形，C1D∥D1A
∵C1D平面AB1E，AB1平面AB1E，
∴C1D∥平面AB1E．
（2）证明：连结B1C，由长方体性质可知，CD⊥平面BC1BC1平面BC1，
∴CD⊥BC1，又AA1=AD，
∴四边形BCC1B1是正方形，BC1⊥B1C，
又B1C∩CD=D，∴BC1⊥平面B1CEB1E平面B1CE，∴BC1⊥B1E．
（3）解：
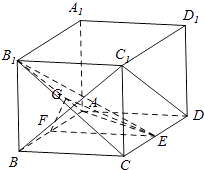
法一：设F是线段AB中点，连结EF
∵EF∥AD，AD⊥平面AA1B1B，
∴EF⊥平面AA1B1B，EF⊥AB1，作FG⊥AB1，EF∩FG=F，
∴AB1⊥平面EFG，AB1⊥EG，∠EGF是二面角E﹣AB1﹣B的平面角，）
直角三角形FGA中，
， 
， 
．
直角三角形EFG中， 
∴二面角E﹣AB1﹣B的正切值 
法二：以A为原点，AB，AD，AA1分别为x，y，z轴建立空间坐标系．
则A（0，0，0）， 
， 
， 
，
， 
， 
，
设平面AB1E的法向量为 
，
由 
， 
， 
， 
，
得： 
，令y=1，得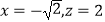 
， 
，
设向量 
与 
的夹角为θ，则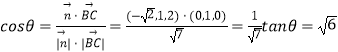 
，
∴二面角E﹣AB1﹣B的正切值为 ．
【解析】（1）推导出四边形B1C1DA是平行四边形，从而C1D∥D1A，由此能证明C1D∥平面AB1E．（2）连结B1C，推导出CD⊥BC1 ， 从而四边形BCC1B1是正方形，BC1⊥B1C，由此能证明BC1⊥B1E．（3）法一：设F是线段AB中点，连结EF，作FG⊥AB1 ， 则∠EGF是二面角E﹣AB1﹣B的平面角，由此能求出二面角E﹣AB1﹣B的正切值．法二：以A为原点，AB，AD，AA1分别为x，y，z轴建立空间坐标系，利用向量法能求出二面角E﹣AB1﹣B的正切值．
【考点精析】通过灵活运用直线与平面平行的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行即可以解答此题．
