题目内容
【题目】选修4-4,极坐标与参数方程
已知在平面直角坐标系![]() 中,
中,![]() 为坐标原点,曲线
为坐标原点,曲线![]() (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,取相同单位长度的极坐标系中,直线
轴的正半轴为极轴,取相同单位长度的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴的交点
轴的交点![]() ,经过点
,经过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
【答案】(1)曲线![]() 的普通方程为
的普通方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)![]() 或
或![]() .
.
【解析】
(1)对曲线![]() 的参数方程两边平方后相加,可求得直角坐标方程.对直线
的参数方程两边平方后相加,可求得直角坐标方程.对直线![]() 的极坐标方程,展开后直接利用极转直的公式进行转化.(2)设出直线
的极坐标方程,展开后直接利用极转直的公式进行转化.(2)设出直线![]() 的参数方程,联立直线
的参数方程,联立直线![]() 与曲线
与曲线![]() 的方程得,利用参数的几何意义列出
的方程得,利用参数的几何意义列出![]() 的方程,由此求得直线的斜率,进而求得倾斜角的值.
的方程,由此求得直线的斜率,进而求得倾斜角的值.
(1)曲线![]() 的普通方程为
的普通方程为![]() ,
,
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)点![]() 的坐标为
的坐标为![]() .设直线
.设直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为倾斜角),联立直线
为倾斜角),联立直线![]() 与曲线
与曲线![]() 的方程得:
的方程得:![]() .
.
设![]() 的参数分别为
的参数分别为![]() ,则
,则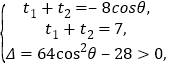
![]()
![]() .
.
![]() 且满足
且满足![]() ,故直线
,故直线![]() 的倾斜解是
的倾斜解是![]() 或
或![]() .
.

【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取![]() 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
分组(岁) | 频数 |
|
|
|
|
|
|
|
|
|
|
合计 |
|
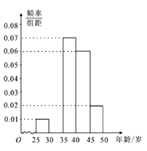
(1)求频率分布表中![]() 、
、![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(2)在抽取的这![]() 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取![]() 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这![]() 人中随机选取
人中随机选取![]() 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这![]() 名市民中年龄在
名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
【题目】随着“互联网+交通”模式的迅猛发展,“共享助力单车”在很多城市相继出现.某“共享助力单车”运营公司为了解某地区用户对该公司所提供的服务的满意度,随机调查了100名用户,得到用户的满意度评分(满分10分),现将评分分为5组,如下表:
组别 | 一 | 二 | 三 | 四 | 五 |
满意度评分 | [0,2) | [2,4) | [4,6) | [6,8) | [8,10] |
频数 | 5 | 10 | a | 32 | 16 |
频率 | 0.05 | b | 0.37 | c | 0.16 |
(1)求表格中的a,b,c的值;
(2)估计用户的满意度评分的平均数;
(3)若从这100名用户中随机抽取25人,估计满意度评分低于6分的人数为多少?
