题目内容
【题目】设椭圆
的离心率为
，以椭圆四个顶点为顶点的四边形的面积为
.
（1）求椭圆E的方程；
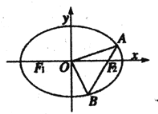
（2）过椭圆E的右焦点
作直线
与E交于A，B两点，O为坐标原点，求
面积的最大值，并求此时直线的方程.
【答案】（1）
；（2）
面积的最大值为
，此时直线
的方程为：
.
【解析】
（1）利用椭圆四个顶点构成的四边形面积、离心率和椭圆
关系可构造方程组求得，进而得到椭圆方程；
（2）①当直线
斜率不存在时，易求得
；②当直线斜率存在时，假设直线方程，与椭圆方程联立得到韦达定理的形式，利用弦长公式求得
，利用点到直线距离公式求出
，从而得到，利用函数求最值的方法可求得的范围；综合两种情况可得最终结果.
（1）
以椭圆四个顶点为顶点的四边形的面积为
，
，
即
…①，又
…②，
…③，
则①②③联立可求得：
，
，
，
椭圆
的方程为：.
（2）①当直线斜率不存在时，则方程为，
，
；
②当直线斜率存在时，可设其方程为：
，由题意可知：
，
由
得：
，
设
，
，则
，
，
，
又原点到直线距离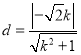
，
，
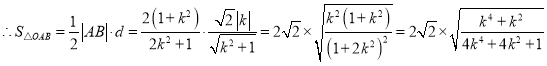
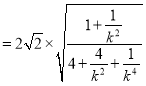令
，则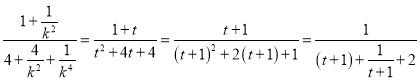
，
，
，
，
，
，
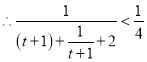综上所述：面积的最大值为，此时直线的方程为：.
练习册系列答案
教材全解字词句篇系列答案
相关题目
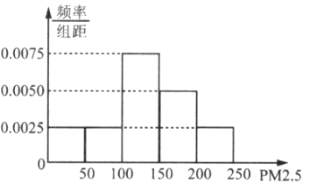
【题目】为了调查某大学学生的某天上网的时间，随机对
名男生和名女生进行了不记名的问卷调查.得到了如下的统计结果：
表1：男生上网时间与频数分布表
上网时间（分钟） |
|
|
|
|
|
人数 |
|
|
|
|
|
表2：女生上网时间与频数分布表
上网时间（分钟） |
|
|
|
|
|
人数 |
|
|
|
|
|
（1）用分层抽样在
选取
人，再随机抽取
人，求抽取的人都是女生的概率；
（2）完成下面的
列联表，并回答能否有
的把握认为“大学生上网时间与性别有关”？
上网时间少于 | 上网时间不少于 | 合计 | |
男生 | |||
女生 | |||
合计 |
附：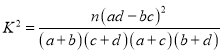
|
|
|
|
|
|
|
|
|
|
|
|
