题目内容
19.已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$是两个不共线的单位向量,夹角为$\frac{2}{3}$π.(1)若向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,求$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值;
(2)若向量$\overrightarrow{a}$+t$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{3}$,求实数t的值.
分析 通过数量积的定义可知$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$|cos<$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$>-$\frac{1}{2}$.(1)利用cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$,计算即得结论;(2)利用$cos\frac{π}{3}$=$\frac{(\overrightarrow{a}+t\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+t\overrightarrow{b}|•|\overrightarrow{a}|}$计算即得结论.
解答 解:由题可知:$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=|$\overrightarrow{{e}_{1}}$|•|$\overrightarrow{{e}_{2}}$|cos<$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$>=$cos\frac{2π}{3}$=-$\frac{1}{2}$.
(1)∵向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,$\overrightarrow{b}$=$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,
∴cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$
=$\frac{(\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})(\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}})}{|\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}}||\overrightarrow{{e}_{1}}-2\overrightarrow{{e}_{2}}|}$
=$\frac{{\overrightarrow{{e}_{1}}}^{2}-2{\overrightarrow{{e}_{2}}}^{2}-\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}}{\sqrt{{\overrightarrow{{e}_{1}}}^{2}+2\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{\overrightarrow{{e}_{2}}}^{2}}•\sqrt{{\overrightarrow{{e}_{1}}}^{2}-4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+4{\overrightarrow{{e}_{2}}}^{2}}}$
=$\frac{1-2-(-\frac{1}{2})}{\sqrt{1+2•(-\frac{1}{2})+1}•\sqrt{1-4•(-\frac{1}{2})+4}}$
=-$\frac{\sqrt{7}}{14}$;
(2)∵向量$\overrightarrow{a}$+t$\overrightarrow{b}$与$\overrightarrow{a}$的夹角为$\frac{π}{3}$,
∴$cos\frac{π}{3}$=$\frac{(\overrightarrow{a}+t\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+t\overrightarrow{b}|•|\overrightarrow{a}|}$
=$\frac{{\overrightarrow{a}}^{2}+t\overrightarrow{a}•\overrightarrow{b}}{\sqrt{{\overrightarrow{a}}^{2}+2t\overrightarrow{a}•\overrightarrow{b}+{t}^{2}{\overrightarrow{b}}^{2}}•\sqrt{{\overrightarrow{a}}^{2}}}$
=$\frac{1}{2}$,
又由(2)知$\overrightarrow{a}•\overrightarrow{b}$=-$\frac{1}{2}$,${\overrightarrow{a}}^{2}$=1,${\overrightarrow{b}}^{2}$=$\sqrt{7}$,
∴$\frac{1}{2}$=$\frac{{\overrightarrow{a}}^{2}+t\overrightarrow{a}•\overrightarrow{b}}{\sqrt{{\overrightarrow{a}}^{2}+2t\overrightarrow{a}•\overrightarrow{b}+{t}^{2}{\overrightarrow{b}}^{2}}•\sqrt{{\overrightarrow{a}}^{2}}}$
=$\frac{1-\frac{1}{2}t}{\sqrt{1-t+7{t}^{2}}}$,
整理得:2t2+t-1=0,
解得:t=-1或t=$\frac{1}{2}$.
点评 本题考查平面向量数量积的运算,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
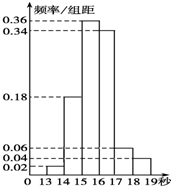 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,平均成绩为z,则从频率分布直方图中可分析出x、y、z的值分别为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:第一组,成绩大于等于13秒且小于14秒;第二组,成绩大于等于14秒且小于15秒;…第六组,成绩大于等于18秒且小于等于19秒.如图是按上述分组方法得到的频率分布直方图.设成绩小于17秒的学生人数占全班总人数的百分比为x,成绩大于等于15秒且小于17秒的学生人数为y,平均成绩为z,则从频率分布直方图中可分析出x、y、z的值分别为( )| A. | 0.9,35,15.86 | B. | 0.9,45,15.5 | C. | 0.1,35,16 | D. | 0.1,45,16.8 |
| A. | $\frac{3}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{16}$ | D. | $\frac{5}{16}$ |
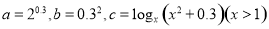 ,则
,则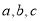 的大小关系是( )
的大小关系是( )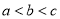 B.
B.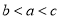
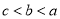 D.
D.