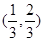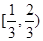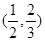题目内容
某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y=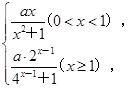 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点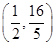 .
.
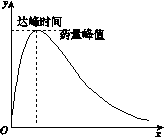
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
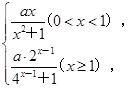 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点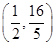 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
(1)y取最大值时,对应的x值为1.(2)3.85小时
(1)由曲线过点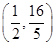 ,可得
,可得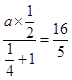 ,故a=8.
,故a=8.
当0<x<1时,y=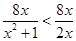 =4,
=4,
当x≥1时,设2x-1=t,可知t≥1,
y=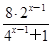 ≤
≤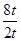 =4(当且仅当t=1,即x=1时,等号成立).
=4(当且仅当t=1,即x=1时,等号成立).
综上可知ymax=4,且当y取最大值时,对应的x值为1.
所以药量峰值为4微克,达峰时间为1小时.
(2)当0<x<1时,由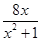 =1,可得x2-8x+1=0,
=1,可得x2-8x+1=0,
解得x=4± ,又4+
,又4+ >1,故x=4-
>1,故x=4- .
.
当x≥1时,设2x-1=t,则t≥1,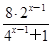 =1,可得
=1,可得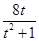 =1,解得t=4±
=1,解得t=4± ,
,
又t≥1,故t=4+ ,所以2x-1=4+
,所以2x-1=4+ ,可得x=log2(4+
,可得x=log2(4+ )+1.
)+1.
由图像知当y≥1时,对应的x的取值范围是[4- ,log2(4+
,log2(4+ )+1],
)+1],
log2(4+ )+1-(4-
)+1-(4- )≈3.85,
)≈3.85,
所以成人按规定剂量服用该药后一次能维持大约3.85小时的有效时间.
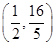 ,可得
,可得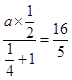 ,故a=8.
,故a=8.当0<x<1时,y=
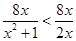 =4,
=4,当x≥1时,设2x-1=t,可知t≥1,
y=
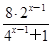 ≤
≤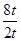 =4(当且仅当t=1,即x=1时,等号成立).
=4(当且仅当t=1,即x=1时,等号成立).综上可知ymax=4,且当y取最大值时,对应的x值为1.
所以药量峰值为4微克,达峰时间为1小时.
(2)当0<x<1时,由
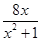 =1,可得x2-8x+1=0,
=1,可得x2-8x+1=0,解得x=4±
 ,又4+
,又4+ >1,故x=4-
>1,故x=4- .
.当x≥1时,设2x-1=t,则t≥1,
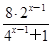 =1,可得
=1,可得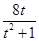 =1,解得t=4±
=1,解得t=4± ,
,又t≥1,故t=4+
 ,所以2x-1=4+
,所以2x-1=4+ ,可得x=log2(4+
,可得x=log2(4+ )+1.
)+1.由图像知当y≥1时,对应的x的取值范围是[4-
 ,log2(4+
,log2(4+ )+1],
)+1],log2(4+
 )+1-(4-
)+1-(4- )≈3.85,
)≈3.85,所以成人按规定剂量服用该药后一次能维持大约3.85小时的有效时间.

练习册系列答案
相关题目
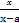 (x≠a).
(x≠a).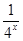 -
-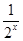 +1的最小值与最大值.
+1的最小值与最大值.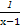 ( )
( )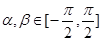 且
且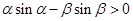 ,则下面结论正确的是( )
,则下面结论正确的是( )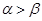
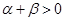
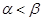
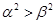
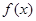 在区间
在区间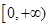 单调递减,则满足
单调递减,则满足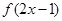
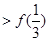 的
的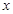 取值范围是( )
取值范围是( )