题目内容
已知f(x)=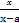 (x≠a).
(x≠a).
(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
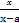 (x≠a).
(x≠a).(1)若a=-2,试证f(x)在(-∞,-2)上单调递增.
(2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.
(1)见解析 (2) (0,1]
(1)任设x1<x2<-2, (0,1]
则f(x1)-f(x2)=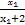 -
-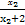 =
=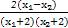 .
.
∵(x1+2)(x2+2)>0,x1-x2<0,
∴f(x1)<f(x2),
∴f(x)在(-∞,-2)上单调递增.
(2)任设1<x1<x2,则
f(x1)-f(x2)=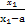 -
-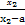
=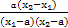 .
.
∵a>0,x2-x1>0,
∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,∴a≤1.
综上所述知a的取值范围是(0,1].
则f(x1)-f(x2)=
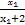 -
-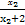 =
=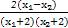 .
.∵(x1+2)(x2+2)>0,x1-x2<0,
∴f(x1)<f(x2),
∴f(x)在(-∞,-2)上单调递增.
(2)任设1<x1<x2,则
f(x1)-f(x2)=
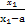 -
-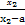
=
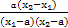 .
.∵a>0,x2-x1>0,
∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,∴a≤1.
综上所述知a的取值范围是(0,1].

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
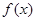 的定义域是
的定义域是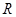 ,对于任意的
,对于任意的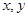 ,有
,有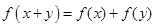 ,且当
,且当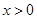 时,
时,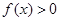 .
.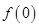 的值;
的值;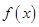 为增函数;
为增函数;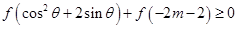 恒成立,求实数
恒成立,求实数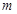 的取值范围.
的取值范围.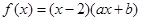 为偶函数,且在
为偶函数,且在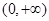 单调递增,则
单调递增,则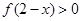 的解集为( )
的解集为( )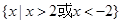

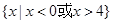

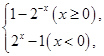 则该函数是( )
则该函数是( )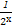 ,若f(x)=
,若f(x)=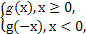 则函数f(x)在定义域内( )
则函数f(x)在定义域内( )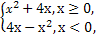 若f(2-a2)>f(a),则实数a的取值范围是( )
若f(2-a2)>f(a),则实数a的取值范围是( )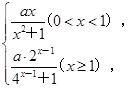 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点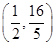 .
.