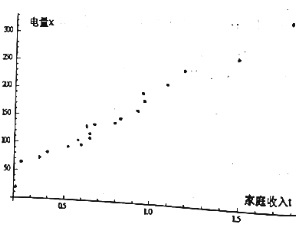
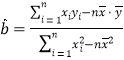题目内容
【题目】设函数f（x）=sin（ωx﹣ 
）+sin（ωx﹣ 
），其中0＜ω＜3，已知f（ ）=0．（12分）
（Ⅰ）求ω；
（Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 
个单位，得到函数y=g（x）的图象，求g（x）在[﹣ ， 
]上的最小值．
【答案】解：（Ⅰ）函数f（x）=sin（ωx﹣ 
）+sin（ωx﹣ 
）
=sinωxcos ﹣cosωxsin ﹣sin（ ﹣ωx）
= 
sinωx﹣ 
cosωx
= 
sin（ωx﹣ 
），
又f（ ）= sin（ ω﹣ ）=0，
∴ ω﹣ =kπ，k∈Z，
解得ω=6k+2，
又0＜ω＜3，
∴ω=2；
（Ⅱ）由（Ⅰ）知，f（x）= sin（2x﹣ ），
将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），得到函数y= sin（x﹣ ）的图象；
再将得到的图象向左平移 
个单位，得到y= sin（x+ ﹣ ）的图象，
∴函数y=g（x）= sin（x﹣ 
）；
当x∈[﹣ ， 
]时，x﹣ ∈[﹣ ， 
]，
∴sin（x﹣ ）∈[﹣ ，1]，
∴当x=﹣ 时，g（x）取得最小值是﹣ × =﹣ ．
【解析】（Ⅰ）利用三角恒等变换化函数f（x）为正弦型函数，根据f（ ）=0求出ω的值；
（Ⅱ）写出f（x）解析式，利用平移法则写出g（x）的解析式，求出x∈[﹣ ， ]时g（x）的最小值．
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识，掌握两角和与差的正弦公式：
，以及对函数y=Asin（ωx+φ）的图象变换的理解，了解图象上所有点向左（右）平移
个单位长度，得到函数
的图象；再将函数的图象上所有点的横坐标伸长（缩短）到原来的
倍（纵坐标不变），得到函数
的图象；再将函数的图象上所有点的纵坐标伸长（缩短）到原来的
倍（横坐标不变），得到函数
的图象．
