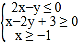题目内容
【题目】设函数f(x)=cos(x+ ![]() ),则下列结论错误的是( )
),则下列结论错误的是( )
A.f(x)的一个周期为﹣2π
B.y=f(x)的图象关于直线x= ![]() 对称
对称
C.f(x+π)的一个零点为x= ![]()
D.f(x)在( ![]() ,π)单调递减
,π)单调递减
【答案】D
【解析】解:A.函数的周期为2kπ,当k=﹣1时,周期T=﹣2π,故A正确,
B.当x= ![]() 时,cos(x+
时,cos(x+ ![]() )=cos(
)=cos( ![]() +
+ ![]() )=cos
)=cos ![]() =cos3π=﹣1为最小值,此时y=f(x)的图象关于直线x=
=cos3π=﹣1为最小值,此时y=f(x)的图象关于直线x= ![]() 对称,故B正确,
对称,故B正确,
C当x= ![]() 时,f(
时,f( ![]() +π)=cos(
+π)=cos( ![]() +π+
+π+ ![]() )=cos
)=cos ![]() =0,则f(x+π)的一个零点为x=
=0,则f(x+π)的一个零点为x= ![]() ,故C正确,
,故C正确,
D.当 ![]() <x<π时,
<x<π时, ![]() <x+
<x+ ![]() <
< ![]() ,此时余弦函数不是单调函数,故D错误,
,此时余弦函数不是单调函数,故D错误,
故选:D
【考点精析】掌握余弦函数的单调性和余弦函数的对称性是解答本题的根本,需要知道余弦函数的单调性:在![]() 上是增函数;在
上是增函数;在![]()
![]() 上是减函数;余弦函数的对称性:对称中心
上是减函数;余弦函数的对称性:对称中心![]() ;对称轴
;对称轴![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
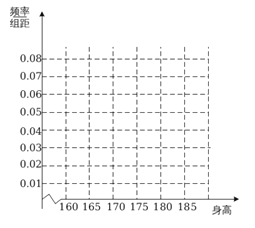
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.