��Ŀ����
����Ŀ��Ϊ��ʵ����ɫ��չ�������˷���Դ��ij�������ƻ��Ծ����õ���ý����շѵķ���.Ϊ�ˣ���ز����ڸ������������![]() ���������·ݵ��õ�������λ��
���������·ݵ��õ�������λ��![]() ���ͼ�ͥ���루��λ����Ԫ�������˽�������м�ͥ�õ��������.
���ͼ�ͥ���루��λ����Ԫ�������˽�������м�ͥ�õ��������.
�õ����������£�
![]() .
.
��Ӧ�ļ�ͥ�����������£�
![]()
![]() .
.
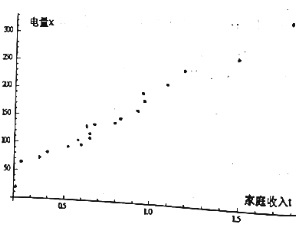
���������ݹ��ҷ���ί��ָʾ�����мƻ�ʵʩ![]() ���ݵ����ʹ
���ݵ����ʹ![]() ���û��ڵ�һ�������Ϊ
���û��ڵ�һ�������Ϊ![]() Ԫ/
Ԫ/![]() ��
��![]() ���û��ڵڶ��������Ϊ
���û��ڵڶ��������Ϊ![]() Ԫ/
Ԫ/![]() ��
��![]() ���û��ڵ����������Ϊ
���û��ڵ����������Ϊ![]() Ԫ/
Ԫ/![]() ������������õ����
������������õ����![]() ���õ���
���õ���![]() ��ĺ�����ϵ��
��ĺ�����ϵ��
�������Լ�ͥ����![]() Ϊ������������
Ϊ������������![]() Ϊ����������ɢ��ͼ����ͼ������
Ϊ����������ɢ��ͼ����ͼ������![]() ����
����![]() �Ļع�ֱ�߷��̣��ع�ֱ�߷��̵�ϵ���������뱣��������.
�Ļع�ֱ�߷��̣��ع�ֱ�߷��̵�ϵ���������뱣��������.
������С���ҵ�������![]() Ԫ����������ϵ������С������֧����Ѷ���Ԫ��
Ԫ����������ϵ������С������֧����Ѷ���Ԫ��
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��һ���������![]() ��
��![]() ������
������![]() �Ļع�ֱ�߷���
�Ļع�ֱ�߷���![]() ��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ
��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ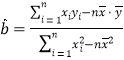 ��
��![]() ������
������![]() ��
��![]() Ϊ������ֵ.
Ϊ������ֵ.
���𰸡�(1)  .
.
(2) ![]() .
.
(3) 72.8Ԫ.
������������������![]()
![]() ��
��![]() ���õ��������еõ���һ�����ٽ�ֵΪ��15����������180���ڶ������ٽ�ֵΪ��19����������260���Ӷ��ɵþ����õ����
���õ��������еõ���һ�����ٽ�ֵΪ��15����������180���ڶ������ٽ�ֵΪ��19����������260���Ӷ��ɵþ����õ����![]() ���õ���
���õ���![]() ��ĺ�����ϵ��
��ĺ�����ϵ��
�����������⣬![]() ��
��![]() �����빫ʽ���㼴����
�����빫ʽ���㼴����
��������ع�ֱ�߷��̼���.
�������I����Ϊ![]() ��
��
���Դ��õ��������еõ���һ�����ٽ�ֵΪ��15����������180��
�ڶ������ٽ�ֵΪ��19����������260����ˣ�

���ԣ�
��II������![]() ��
��
![]() ��
��
 ��
��
����![]() ��
��
�Ӷ��ع�ֱ�߷���Ϊ![]() ��
��
����![]() ʱ��
ʱ��![]() ��
��
![]() �����ԣ�С������֧�����72.8Ԫ��
�����ԣ�С������֧�����72.8Ԫ��
��ܰ��ʾ������ѧ���ֹ����㣬�������������������ļ�������������ʦ����۷֡�����ڣ�����0���ڣ������������ڡ�3����������0�����

����Ŀ��ij��ѧ�Ӹ��������������ȡn��ѧ�������ߣ��������������õ���Ƶ�ʷֲ��������ʾ��
��� | ���� | Ƶ�� | Ƶ�� |
��1�� |
| 5 | 0.05 |
��2�� |
| a | 0.35 |
��3�� |
| 30 | b |
��4�� |
| 20 | 0.20 |
��5�� |
| 10 | 0.10 |
�ϼ� | n | 1.00 | |
��1�����Ƶ�ʷֲ�����![]() ��ֵ�����������Ƶ�ʷֲ�ֱ��ͼ��
��ֵ�����������Ƶ�ʷֲ�ֱ��ͼ��
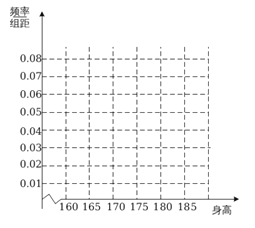
��2��Ϊ���ܶ�ѧ������������һ���˽⣬��У�����ڵ�1��4��5�����÷ֲ����ȡ7��ѧ�����в�ͬ��Ŀ�����ܲ��ԣ�������7��ѧ���������ȡ2��ѧ�������������ϲ��ԣ����4����������һ��ѧ�������еĸ���.