题目内容
已知双曲线的右准线为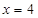 ,右焦点
,右焦点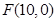 ,离心率
,离心率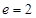 ,求双曲线方程.
,求双曲线方程.
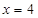 ,右焦点
,右焦点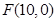 ,离心率
,离心率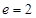 ,求双曲线方程.
,求双曲线方程.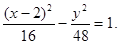
【错解分析】错解一:
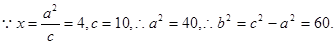 故所求的双曲线方程为
故所求的双曲线方程为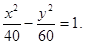
错解二: 由焦点
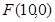 知
知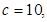
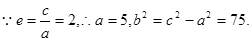
故所求的双曲线方程为
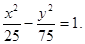
【正解】法一: 设
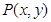 为双曲线上任意一点,因为双曲线的右准线为
为双曲线上任意一点,因为双曲线的右准线为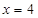 ,右焦点
,右焦点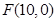 ,离心率
,离心率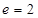 ,由双曲线的定义知
,由双曲线的定义知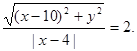 整理得
整理得 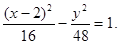
解法二: 依题意,设双曲线的中心为
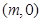 ,
,则
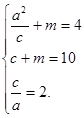 解得
解得 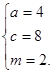 ,所以
,所以 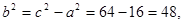
故所求双曲线方程为
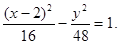

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
题目内容
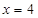 ,右焦点
,右焦点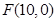 ,离心率
,离心率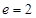 ,求双曲线方程.
,求双曲线方程.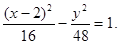
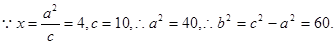 故所求的双曲线方程为
故所求的双曲线方程为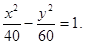
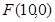 知
知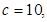
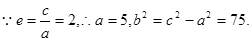
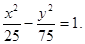
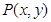 为双曲线上任意一点,因为双曲线的右准线为
为双曲线上任意一点,因为双曲线的右准线为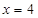 ,右焦点
,右焦点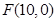 ,离心率
,离心率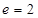 ,由双曲线的定义知
,由双曲线的定义知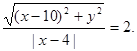 整理得
整理得 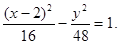
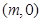 ,
,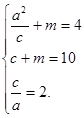 解得
解得 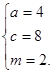 ,所以
,所以 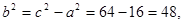
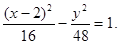

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案