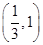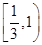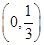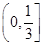题目内容
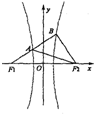
如图,F1,F2是双曲线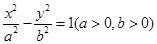 的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为
的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为
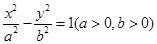 的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为
的左、右焦点,过F1的直线l与C的左、右两支分别交于A,B两点.若|AB|:|BF2|:|AF2|=3:4:5,则双曲线的离心率为
A.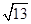 | B.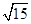 | C.2 | D.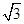 |
A
试题分析:设|AB|=3,则BF2|=4,|AF2|=5,所以△ABF2中,
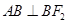 ,,由双曲线的第一定义知2a=
,,由双曲线的第一定义知2a=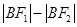 =
= ,∴
,∴ ,∴
,∴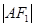 =3.∴
=3.∴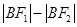 | =3+3-4=2a,∴a=1.在Rt
| =3+3-4=2a,∴a=1.在Rt 中,
中, =52,∴c=
=52,∴c=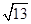 ,∴双曲线的离心率e=
,∴双曲线的离心率e=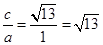
点评:求解圆锥曲线的离心率问题关键是通过定义、条件等找到有关a,b,c的方程,然后求出离心率即可

练习册系列答案
相关题目
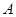 是椭圆
是椭圆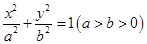 的右顶点,若点
的右顶点,若点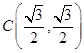 在椭圆上,且满足
在椭圆上,且满足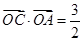 .(其中
.(其中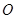 为坐标原点)
为坐标原点)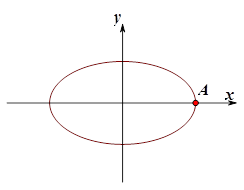
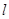 与椭圆交于两点
与椭圆交于两点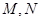 ,当
,当 时,求
时,求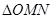 面积的最大值.
面积的最大值.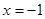 相切。记动点P的轨迹为C。
相切。记动点P的轨迹为C。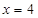 ,右焦点
,右焦点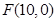 ,离心率
,离心率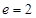 ,求双曲线方程.
,求双曲线方程.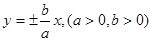 ,若双曲线上有一点M(
,若双曲线上有一点M(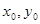 ),使
),使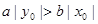 ,那双曲线的交点( )。
,那双曲线的交点( )。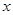 轴上
轴上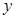 轴上
轴上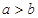 时在
时在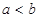 时在
时在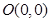 的距离是到定点
的距离是到定点 距离的二倍,求这条曲线的方程.
距离的二倍,求这条曲线的方程.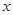 轴上的椭圆
轴上的椭圆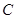 过点
过点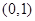 ,且离心率为
,且离心率为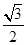 ,
,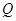 为椭圆
为椭圆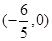 的直线
的直线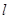 与椭圆
与椭圆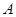 ,
,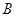 两点.
两点.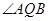 的大小;
的大小;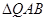 为等腰三角形?如果存在,求出直线
为等腰三角形?如果存在,求出直线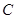 方程为
方程为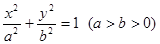 ,左、右焦点分别是
,左、右焦点分别是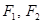 ,若椭圆
,若椭圆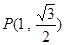 到
到 .
. 是椭圆
是椭圆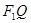 中点
中点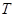 的轨迹方程;
的轨迹方程;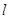 过定点
过定点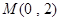 ,且与椭圆
,且与椭圆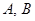 ,若
,若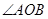 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线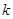 的取值范围.
的取值范围.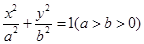 中,
中,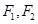 分别是其左右焦点,若
分别是其左右焦点,若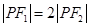 ,则该椭圆离心率的取值范围是 ( )
,则该椭圆离心率的取值范围是 ( )