Question

【题目】关于的方程组的系数矩阵记为，且该方程组存在非零解，若存在三阶矩阵，使得，（0表示零矩阵，即所有元素均为0的矩阵；矩阵对应的行列式为），则

（1）一定为1；

（2）一定为0；

（3）该方程组一定有无穷多解.

其中正确说法的个数是（ ）

A.0B.1C.2D.3

Answer 1

【答案】D

【解析】

先根据方程组有非零解可得，由此可得的值及方程组有无穷多组解，故可判断（1）、（3）的正误，用反证法可证，故（2）正确，从而可得正确的选项.

由题设有，因为方程组存在非零解，故，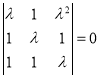

而，故 ，故（1）正确.

因，故方程组由三个相同的方程构成即，

它有无数组解，故（3）正确.

若，则有可逆矩阵，从而（0表示零矩阵）即（0表示零矩阵），

与矛盾，故（2）正确.

故选：D.