题目内容
9.在数列{an}中,已知a1=1,an+2=$\frac{1}{{{a_n}+1}}$,a100=a96,则a11+a12=$\frac{3}{26}±\frac{{\sqrt{5}}}{2}$.分析 通过a1=1、an+2=$\frac{1}{{{a_n}+1}}$计算可知a11=$\frac{8}{13}$,利用a96=a100=$\frac{1}{{a}_{98}+1}$=$\frac{1}{\frac{1}{{a}_{96}}+1}$计算可知a96=$\frac{±\sqrt{5}-1}{2}$,通过$\frac{±\sqrt{5}-1}{2}$=$\frac{1}{\frac{±\sqrt{5}-1}{2}+1}$可知a2n=$\frac{±\sqrt{5}-1}{2}$,进而计算可得结论.
解答 解:∵a1=1,an+2=$\frac{1}{{{a_n}+1}}$,
∴${a}_{3}=\frac{1}{{a}_{1}+1}$=$\frac{1}{2}$,
${a}_{5}=\frac{1}{{a}_{3}+1}$=$\frac{1}{1+\frac{1}{2}}$=$\frac{2}{3}$,
${a}_{7}=\frac{1}{{a}_{5}+1}$=$\frac{1}{\frac{2}{3}+1}$=$\frac{3}{5}$,
${a}_{9}=\frac{1}{{a}_{7}+1}$=$\frac{1}{\frac{3}{5}+1}$=$\frac{5}{8}$,
${a}_{11}=\frac{1}{{a}_{9}+1}$=$\frac{1}{\frac{5}{8}+1}$=$\frac{8}{13}$,
∵a100=a96,
∴a100=a96=$\frac{1}{{a}_{98}+1}$=$\frac{1}{\frac{1}{{a}_{96}}+1}$,
整理得:${{a}_{96}}^{2}$+a96-1=0,
解得:a96=$\frac{\sqrt{5}-1}{2}$或a96=$\frac{-\sqrt{5}-1}{2}$,
∵$\frac{\sqrt{5}-1}{2}$=$\frac{2}{\sqrt{5}+1}$=$\frac{1}{\frac{\sqrt{5}-1}{2}+1}$,$\frac{-\sqrt{5}-1}{2}$=$\frac{2}{-\sqrt{5}+1}$=$\frac{1}{\frac{-\sqrt{5}-1}{2}+1}$,
∴a2n=$\frac{\sqrt{5}-1}{2}$或a2n=$\frac{-\sqrt{5}-1}{2}$,即a2n=$\frac{±\sqrt{5}-1}{2}$,
∴a12=$\frac{±\sqrt{5}-1}{2}$,
∴a11+a12=$\frac{8}{13}$+$\frac{±\sqrt{5}-1}{2}$=$\frac{3}{26}±\frac{{\sqrt{5}}}{2}$,
故答案为:$\frac{3}{26}±\frac{{\sqrt{5}}}{2}$.
点评 本题主要考查数列递推公式的应用,根据递推公式分别求出a11、a12的值是解决本题的关键,综合性较强,难度较大,注意解题方法的积累,属于难题.

| A. | $\frac{1}{1024}$ | B. | $\frac{1}{512}$ | C. | $\frac{1}{2048}$ | D. | 1 |
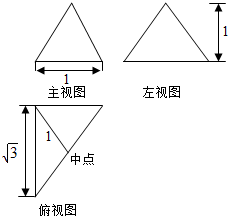
| A. | $\frac{32}{3}π$ | B. | $\frac{{8\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{{\sqrt{2}}}{3}π$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |

| A. | 16$\sqrt{2}$ | B. | 16+16$\sqrt{2}$ | C. | 32$\sqrt{2}$ | D. | 16+32$\sqrt{2}$ |
| A. | (-4,2) | B. | (-2,4) | C. | (-∞,-4]∪[2,+∞) | D. | (-∞,-2]∪[4,+∞) |
| A. | y=($\sqrt{x}$)2 | B. | y=$\root{3}{{x}^{3}}$ | C. | y=$\sqrt{x^2}$ | D. | y=$\frac{{x}^{2}}{x}$ |