题目内容
14.函数y=f(x)满足下列条件:①定义域是R
②图象关于直线x=1对称
③在区间[2,+∞)是增函数
试写出满足上述条件的一个y=f(x)解析式 f(x)=y=|x-1|+2.或y=(x-1)2+2 (写出任意一个即可)
分析 利用已知条件,直接推出结果即可.
解答 解:①定义域是R
②图象关于直线x=1对称;
③在区间[2,+∞)是增函数;
满足条件一个函数可以为:y=|x-1|+2.或y=(x-1)2+2等等.
故答案为:y=|x-1|+2.或y=(x-1)2+2.
点评 本题考查函数的简单性质的应用,函数的解析式的求法,考查判断能力.

练习册系列答案
相关题目
2.命题p:“a>0且b>0”,命题q:“方程$\frac{x^2}{a}+\frac{y^2}{b}=1$表示椭圆”,那么p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.若函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y)成立,则f(0)=( )
| A. | 0 | B. | 1 | C. | -1 | D. | 不能确定 |
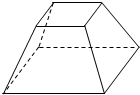 (1)画出如图的三视图.
(1)画出如图的三视图.