题目内容
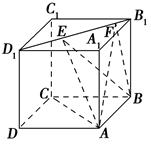
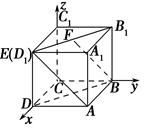
如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F且EF=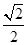 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).
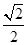 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).
| A.AC⊥BE |
| B.EF∥平面ABCD |
| C.三棱锥A-BEF的体积为定值 |
| D.异面直线AE,BF所成的角为定值 |
D
∵AC⊥平面BB1D1D,又BE?平面BB1,D1D.
∴AC⊥BE,故A正确.
∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,
∴EF∥平面ABCD,故B正确.
C中由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为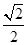 ,故VA-BEF为定值.
,故VA-BEF为定值.
当点E在D1处,点F为D1B1的中点时,建立空间直角坐标系,如图所示,可得A(1,1,0),B(0,1,0),E(1,0,1),F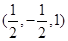 ,
,
∴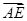 =(0,-1,1),
=(0,-1,1),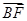 =
=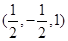 ,
,
∴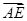 ·
·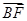 =
=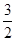 .
.
又|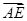 |=
|= ,|
,|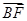 |=
|=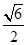 ,
,
∴cos〈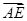 ,
,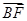 〉=
〉=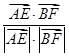 =
=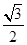 .
.
∴此时异面直线AE与BF成30°角.
②当点E为D1B1的中点,点F在B1处时,此时E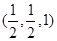 ,F(0,1,1),
,F(0,1,1),
∴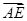 =
=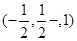 ,
,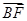 =(0,0,1),
=(0,0,1),
∴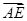 ·
·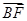 =1,|
=1,|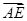 |=
|=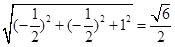 ,
,
∴cos〈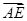 ,
,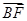 〉=
〉=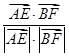 =
=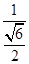 =
=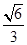 ≠
≠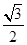 ,故选D.
,故选D.
∴AC⊥BE,故A正确.
∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,
∴EF∥平面ABCD,故B正确.
C中由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为
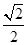 ,故VA-BEF为定值.
,故VA-BEF为定值.当点E在D1处,点F为D1B1的中点时,建立空间直角坐标系,如图所示,可得A(1,1,0),B(0,1,0),E(1,0,1),F
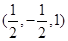 ,
,
∴
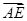 =(0,-1,1),
=(0,-1,1),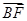 =
=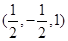 ,
,∴
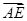 ·
·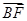 =
=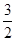 .
.又|
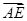 |=
|= ,|
,|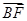 |=
|=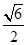 ,
,∴cos〈
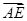 ,
,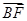 〉=
〉=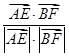 =
=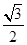 .
.∴此时异面直线AE与BF成30°角.
②当点E为D1B1的中点,点F在B1处时,此时E
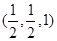 ,F(0,1,1),
,F(0,1,1),∴
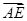 =
=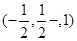 ,
,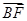 =(0,0,1),
=(0,0,1),∴
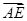 ·
·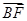 =1,|
=1,|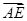 |=
|=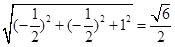 ,
,∴cos〈
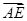 ,
,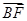 〉=
〉=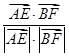 =
=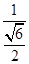 =
=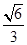 ≠
≠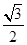 ,故选D.
,故选D.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
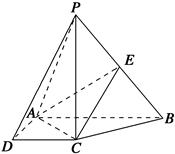
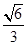 ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值. ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.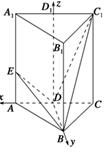
 为直角梯形,
为直角梯形,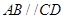 ,
,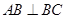 ,
,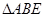 为等边三角形,且平面
为等边三角形,且平面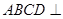 平面
平面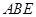 ,
,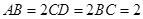 ,
,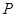 为
为 中点.
中点.
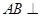
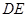 ;
;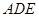 与平面
与平面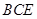 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;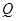 ,使
,使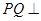 平面
平面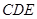 ,如果存在,求
,如果存在,求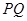 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 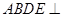 平面
平面 ,
,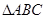 是等腰直角三角形,
是等腰直角三角形,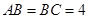 ,四边形
,四边形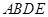 是直角梯形,
是直角梯形,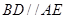 ,
,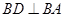 ,
,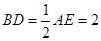 ,点
,点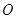 、
、 分别为
分别为 、
、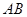 的中点.
的中点.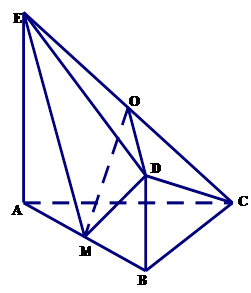
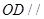 平面
平面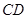 和平面
和平面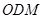 所成角的正弦值;
所成角的正弦值;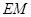 上找到一点
上找到一点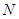 ,使得
,使得 平面
平面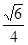 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.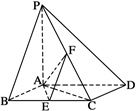
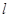 的法向量为
的法向量为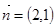 ,则该直线的倾斜角为 .(用反三角函数值表示)
,则该直线的倾斜角为 .(用反三角函数值表示)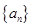 的前n项和为
的前n项和为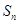 ,且
,且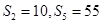 ,则过点
,则过点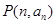 和
和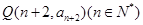 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )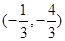
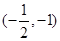
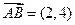 ,
, 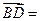 (-3,-5)则
(-3,-5)则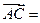 ( )
( )