题目内容
在正三棱柱ABC-A1B1C1中,AB=2,AA1=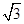 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.
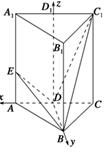
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.
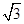 ,点D为AC的中点,点E在线段AA1上.
,点D为AC的中点,点E在线段AA1上.
(1)当AE∶EA1=1∶2时,求证DE⊥BC1;
(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.
(1)见解析(2)存在
(1)证明:连接DC1,因为ABC-A1B1C1为正三棱柱,所以△ABC为正三角形,又因为D为AC的中点,所以BD⊥AC,又平面ABC⊥平面ACC1A1,所以BD⊥平面ACC1A1,所以BD⊥DE.因为AE∶EA1=1∶2,AB=2,AA1=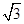 ,所以AE=
,所以AE=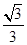 ,AD=1,所以在Rt△ADE中,∠ADE=30°,在Rt△DCC1中,∠C1DC=60°,所以∠EDC1=90°,即ED⊥DC1,又BD∩DC1=D,所以ED⊥平面BDC1,BC1?面BDC1,所以ED⊥BC1.
,AD=1,所以在Rt△ADE中,∠ADE=30°,在Rt△DCC1中,∠C1DC=60°,所以∠EDC1=90°,即ED⊥DC1,又BD∩DC1=D,所以ED⊥平面BDC1,BC1?面BDC1,所以ED⊥BC1.
(2)解 假设存在点E满足条件,设AE=h.
取A1C1的中点D1,连接DD1,则DD1⊥平面ABC,所以DD1⊥AD,DD1⊥BD,分别以DA,DB,DD1所在直线为x,y,z轴建立空间直角坐标系D-xyz,则A(1,0,0),B(0,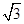 ,0),E(1,0,h),所以
,0),E(1,0,h),所以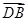 =(0,
=(0,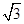 ,0),
,0), =(1,0,h),
=(1,0,h), =(-1,
=(-1,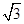 ,0),
,0), =(0,0,h),设平面DBE的一个法向量为n1=(x1,y1,z1),
=(0,0,h),设平面DBE的一个法向量为n1=(x1,y1,z1),
则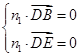 ,
, 令z1=1,得n1=(-h,0,1),同理,平面ABE的一个法向量为n2=(x2,y2,z2),则
令z1=1,得n1=(-h,0,1),同理,平面ABE的一个法向量为n2=(x2,y2,z2),则 ,
,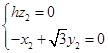 ∴n2=(
∴n2=(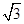 ,1,0).
,1,0).
∴cos〈n1,n2〉=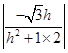 =cos 60°=
=cos 60°= .解得h=
.解得h=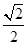 <
<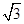 ,故存在点E,当AE=
,故存在点E,当AE=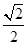 时,二面角D-BE-A等于60°.
时,二面角D-BE-A等于60°.
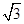 ,所以AE=
,所以AE=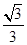 ,AD=1,所以在Rt△ADE中,∠ADE=30°,在Rt△DCC1中,∠C1DC=60°,所以∠EDC1=90°,即ED⊥DC1,又BD∩DC1=D,所以ED⊥平面BDC1,BC1?面BDC1,所以ED⊥BC1.
,AD=1,所以在Rt△ADE中,∠ADE=30°,在Rt△DCC1中,∠C1DC=60°,所以∠EDC1=90°,即ED⊥DC1,又BD∩DC1=D,所以ED⊥平面BDC1,BC1?面BDC1,所以ED⊥BC1.(2)解 假设存在点E满足条件,设AE=h.
取A1C1的中点D1,连接DD1,则DD1⊥平面ABC,所以DD1⊥AD,DD1⊥BD,分别以DA,DB,DD1所在直线为x,y,z轴建立空间直角坐标系D-xyz,则A(1,0,0),B(0,
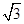 ,0),E(1,0,h),所以
,0),E(1,0,h),所以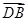 =(0,
=(0,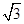 ,0),
,0), =(1,0,h),
=(1,0,h), =(-1,
=(-1,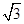 ,0),
,0), =(0,0,h),设平面DBE的一个法向量为n1=(x1,y1,z1),
=(0,0,h),设平面DBE的一个法向量为n1=(x1,y1,z1),则
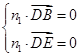 ,
, 令z1=1,得n1=(-h,0,1),同理,平面ABE的一个法向量为n2=(x2,y2,z2),则
令z1=1,得n1=(-h,0,1),同理,平面ABE的一个法向量为n2=(x2,y2,z2),则 ,
,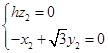 ∴n2=(
∴n2=(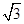 ,1,0).
,1,0).∴cos〈n1,n2〉=
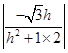 =cos 60°=
=cos 60°= .解得h=
.解得h=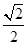 <
<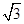 ,故存在点E,当AE=
,故存在点E,当AE=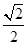 时,二面角D-BE-A等于60°.
时,二面角D-BE-A等于60°.
练习册系列答案
相关题目
 中,底面
中,底面 为矩形,
为矩形, 为等边三角形,
为等边三角形,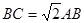 ,点
,点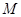 为
为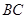 中点,平面
中点,平面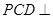 平面
平面
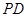 和
和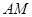 所成角的余弦值;
所成角的余弦值;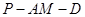 的大小.
的大小.
 .
.
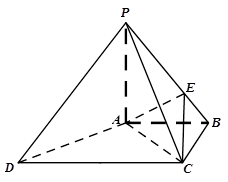
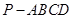 中,
中,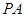 ⊥平面
⊥平面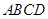 ,底面
,底面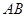 ∥
∥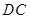 ,
,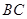 ,
,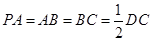 ,点
,点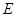 在棱
在棱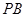 上,且
上,且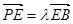 .
.
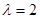 时,求证:
时,求证: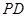 ∥面
∥面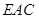 ;
;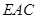 所成角为
所成角为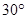 ,求实数
,求实数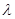 的值.
的值.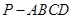 中,底面
中,底面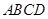 是边长为
是边长为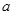 的正方形,侧面
的正方形,侧面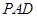
 底面
底面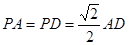 .
.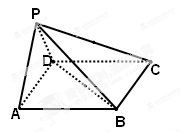
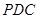 ;
; 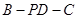 的余弦值.
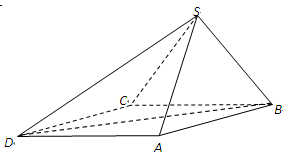
的余弦值.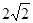 ,SA=SB=
,SA=SB=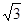 。
。
 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).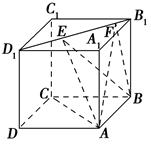
 (-1,2)
(-1,2)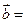 (1,-2),则
(1,-2),则 与
与 的坐标分别是( )
的坐标分别是( )