题目内容
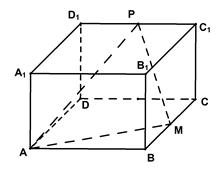
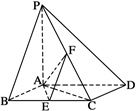
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点。
(Ⅰ)求证:AE⊥PD;
(Ⅱ)若直线PB与平面PAD所成角的正弦值为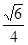 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.
(Ⅰ)求证:AE⊥PD;
(Ⅱ)若直线PB与平面PAD所成角的正弦值为
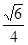 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.
(1)见解析
(2)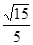
(2)
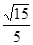
(Ⅰ)要证AE⊥PD ,先证AE⊥平面PAD,需要证明PA⊥AE,转化为证PA⊥平面ABCD;(Ⅱ)建立坐标系计算二面角E-AF-C的余弦值.
(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE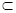 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而PA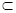 平面PAD,AD
平面PAD,AD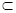 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD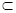 平面PAD.所以 AE⊥PD. 6分
平面PAD.所以 AE⊥PD. 6分
(Ⅱ)解:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,
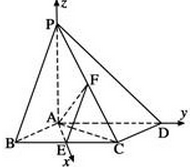
设AB=2,AP=a,则A(0,0,0),B(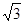 ,-1,0),C(
,-1,0),C(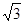 ,1,0),D(0,2,0),P(0,0,a),E(
,1,0),D(0,2,0),P(0,0,a),E(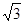 ,0,0),F(
,0,0),F(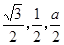 ),
),
所以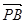 =(
=(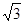 ,-1,-a),且
,-1,-a),且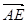 =(
=(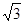 ,0,0)为平面PAD的法向量,设直线PB与平面PAD所成的角为θ,
,0,0)为平面PAD的法向量,设直线PB与平面PAD所成的角为θ,
由sinθ=|cos<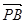 ,
,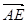 >|=
>|=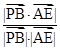 =
=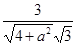 =
=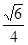 8分
8分
解得a="2" 所以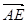 =(
=(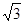 ,0,0),
,0,0),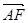 =(
=(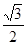 ,
,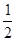 ,1)
,1)
设平面AEF的一法向量为m=(x1,y1,z1),则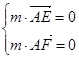 ,因此
,因此 取z1=-1,则m=(0,2,-1), 10分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故
取z1=-1,则m=(0,2,-1), 10分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故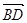 为平面AFC的一法向量.又
为平面AFC的一法向量.又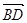 =(-
=(-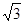 ,3,0),
,3,0),
所以cos<m,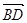 >=
>=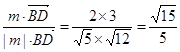 .
.
因为二面角E-AF-C为锐角,所以所求二面角的余弦值为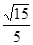 .
.
(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE
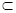 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.而PA
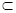 平面PAD,AD
平面PAD,AD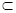 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,所以 AE⊥平面PAD,又PD
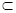 平面PAD.所以 AE⊥PD. 6分
平面PAD.所以 AE⊥PD. 6分(Ⅱ)解:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,

设AB=2,AP=a,则A(0,0,0),B(
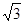 ,-1,0),C(
,-1,0),C(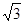 ,1,0),D(0,2,0),P(0,0,a),E(
,1,0),D(0,2,0),P(0,0,a),E(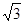 ,0,0),F(
,0,0),F(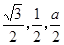 ),
),所以
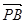 =(
=(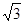 ,-1,-a),且
,-1,-a),且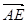 =(
=(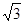 ,0,0)为平面PAD的法向量,设直线PB与平面PAD所成的角为θ,
,0,0)为平面PAD的法向量,设直线PB与平面PAD所成的角为θ,由sinθ=|cos<
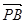 ,
,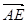 >|=
>|=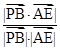 =
=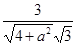 =
=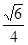 8分
8分解得a="2" 所以
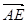 =(
=(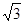 ,0,0),
,0,0),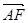 =(
=(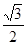 ,
,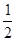 ,1)
,1)设平面AEF的一法向量为m=(x1,y1,z1),则
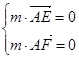 ,因此
,因此 取z1=-1,则m=(0,2,-1), 10分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故
取z1=-1,则m=(0,2,-1), 10分 因为BD⊥AC,BD⊥PA,PA∩AC=A,所以BD⊥平面AFC,故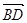 为平面AFC的一法向量.又
为平面AFC的一法向量.又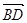 =(-
=(-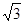 ,3,0),
,3,0),所以cos<m,
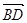 >=
>=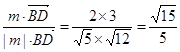 .
.因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
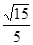 .
.
练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
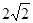 ,SA=SB=
,SA=SB=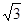 。
。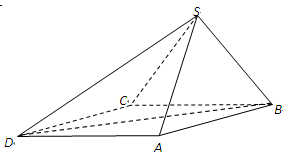
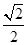 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).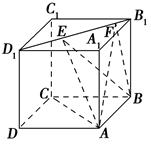
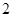 的正方体
的正方体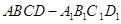 中,
中,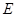 、
、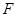 分别是
分别是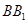 、
、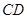 的中点,试用向量的方法:
的中点,试用向量的方法: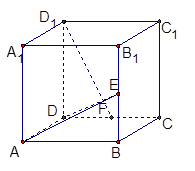
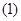 求证:
求证: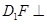 平面
平面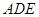 ;
;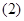 求
求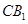 与平面
与平面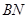 ⊥平面
⊥平面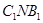 (2)求平面
(2)求平面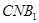 与平面
与平面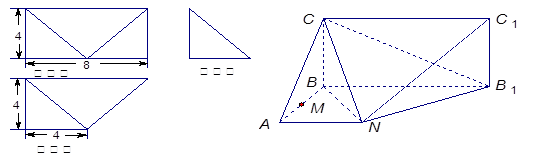
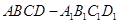 中,
中,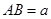 ,
,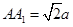 ,
,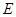 为
为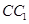 的中点,
的中点,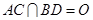 .
.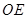 ∥平面
∥平面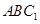 ;
;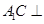 平面
平面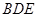 .
.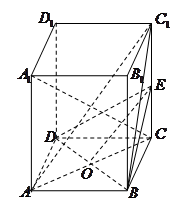
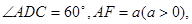 (I)求证:AC⊥BF;
(I)求证:AC⊥BF;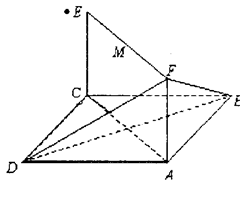
 B
B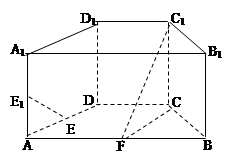
 中,
中,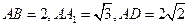 ,
, 为
为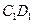 的中点,
的中点,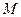 为
为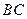 的中点。
的中点。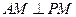 ;
;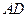 与平面
与平面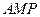 所成角的正弦值。
所成角的正弦值。